题目内容
10.已知直线l:xcosθ+(y-2)sinθ=1,当θ取不同的值时,它是一系列直线l1,l2,l3,…称为直线系,则下列说法正确的序号是②③④.①直线系恒过顶点(0,2);
②直线系与圆x2+(y-2)2=1相切;
③存在一定点不在直线系的任何直线上;
④存在四条直线围成一个正方形;
⑤若直线系中某三直线围成等边三角形,则这个三角形面积是定值.
分析 ①把点的坐标代人直线方程验证该直线系是否过定点即可;
②求出圆心到直线的距离d,与圆的半径r比较即可;
③验证定点(0,2)的坐标不满足直线方程,即得结论;
④求出cosθ=0时对应的直线方程和sinθ=0时对应的直线方程,四条直线围成一个正方形;
⑤由②知,直线xcosθ+(y-2)sinθ=1与圆x2+(y-2)2=1相切,是该圆的所有切线,
该圆可以是一个正三角形的内切圆,也可以是一个正三角形的旁切圆,所以面积有两种情况,不是定值.
解答 解:对于①,直线l:xcosθ+(y-2)sinθ=1,
当x=0,y=2时,0≠1,∴该直线系不过定点(0,2),①错误;
对于②,圆心(0,2)到直线xcosθ+ysinθ-2sinθ-1=0的距离是
d=$\frac{|2sinθ-2sinθ-1|}{\sqrt{{cos}^{2}θ{+sin}^{2}θ}}$=1=r,
∴直线系与圆x2+(y-2)2=1相切,②正确;
对于③,存在一定点(0,2),该点的坐标不满足直线方程,
∴该点不在直线系的任何直线上,③正确;
对于④,当cosθ=0时,sinθ=±1,此时y=3或y=1;
当sinθ=0时,cosθ=±1,此时x=±1;
∴存在四条直线x=±1和y=3或y=1,围成一个正方形,④正确;
对于⑤,由②知,点(0,2)到直线xcosθ+(y-2)sinθ=1的距离d=1,
∴这组直线与圆x2+(y-2)2=1相切,
该圆可以是一个正三角形的内切圆,也可以是一个正三角形的旁切圆,
∴三角形的面积有两种情况,⑤错误.
综上,正确的命题序号是②③④.
故答案为:②③④.
点评 本题考查了直线与圆的综合应用问题,也考查了数形结合思想的应用问题,是综合性题目.

练习册系列答案
相关题目
18.若m>n,则( )
| A. | 0.2m<0.2n | B. | log0.3m>log0.3n | C. | 2m<2n | D. | m2>n2 |
5.从集合{1,2,3,4,5,6}中随机抽取一个数a,从集合{1,2,3}中随机收取一个数b,则loga2b=1的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
2.若$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(4,k),$\overrightarrow{c}$=$\overrightarrow{0}$,则($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=( )
| A. | 0 | B. | $\overrightarrow{0}$ | C. | 4+2k | D. | 8+k |
19.已知数列$\frac{1}{1×2},\frac{1}{2×3},\frac{1}{3×4},…,\frac{1}{{n×({n+1})}},…$,下面各数中是此数列中的项的是( )
| A. | $\frac{1}{35}$ | B. | $\frac{1}{42}$ | C. | $\frac{1}{48}$ | D. | $\frac{1}{54}$ |
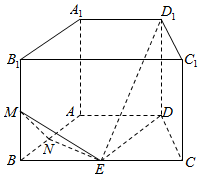 如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.
如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.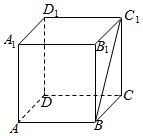 如图所示,在正方体ABCD-A1B1C1D1中,
如图所示,在正方体ABCD-A1B1C1D1中,