题目内容
若函数y=f(x)满足f(a+x)+f(a-x)=2b(其中a,b不同时为0),则称函数y=f(x)为“准奇函数”,称点(a,b)为函数f(x)的“中心点”.现有如下命题:
①函数f(x)=sinx+1是准奇函数;
②若准奇函数y=f(x)在R上的“中心点”为(a,f(a)),则函数F(x)=f(x+a)-f(a)不是R上的奇函数;
③已知函数f(x)=x3-3x2+6x-2是准奇函数,则它的“中心点”为(1,2);
④已知函数f(x)=2x-cosx为“准奇函数”,数列{an}是公差为
的等差数列,若
f(an)=7π(其中
ai表示
ai=a1+a2+…+an),则
=
其中正确的命题是 .(写出所有正确命题的序号)
①函数f(x)=sinx+1是准奇函数;
②若准奇函数y=f(x)在R上的“中心点”为(a,f(a)),则函数F(x)=f(x+a)-f(a)不是R上的奇函数;
③已知函数f(x)=x3-3x2+6x-2是准奇函数,则它的“中心点”为(1,2);
④已知函数f(x)=2x-cosx为“准奇函数”,数列{an}是公差为
| π |
| 8 |
| 7 |
 |
| n=1 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| [f(a4)]2 |
| a1•a7 |
| 64 |
| 7 |
其中正确的命题是
考点:抽象函数及其应用
专题:函数的性质及应用
分析:①f(0+x)+f(0-x)=2,得a=0,b=1,满足“准奇函数”的定义,
②根据函数“准奇函数”的定义,利用函数奇偶性的定义即可证明函数F(x)=f(x+a)-f(a)为R上的奇函数.
③f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,得点(1,2)为函数f(x)的“中心点”,
④根据等差数列的通项公式,求出a1,a4,a7的值,代入进行求解即可.
②根据函数“准奇函数”的定义,利用函数奇偶性的定义即可证明函数F(x)=f(x+a)-f(a)为R上的奇函数.
③f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,得点(1,2)为函数f(x)的“中心点”,
④根据等差数列的通项公式,求出a1,a4,a7的值,代入进行求解即可.
解答:
解:①∵函数f(x)=sinx+1,∴f(0+x)+f(0-x)=2,∴a=0,b=1,满足“准奇函数”的定义,故①正确;
②若F(x)=f(x+a)-f(a),则F(-x)+F(x)=f(x+a)-f(a)+f(-x+a)-f(a)=f(a-x)+f(a+x)-2f(a),
∵f(x)在R上的“中心点”为(a,f(a)),
∴f(a-x)+f(a+x)=2f(a),
即F(-x)+F(x)=f(a-x)+f(a+x)-2f(a)=0,
∴F(-x)=-F(x),∴函数F(x)=f(x+a)-f(a)为R上的奇函数,∴②错误.
③函数f(x)=x3-3x2+6x-2,∴f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,
∴点(1,2)为函数f(x)的“中心点”,③正确;
④f(x)=2x-cosx,
∴f(a1)+f(a2)+…+f(a7)=2(a1+a2+…+a7)-(cosa1+cosa2+…+cosa7),
∵{an}是公差d=
的等差数列,
∴a1+a2+…+a7=7a4,
cosa1+cosa2+…+cosa7=cos(a4-3d)+cos(a4-2d)+(cos(a4-d)+cosd+cos(a4+d)+cos(a4+2d)+cos(a4+3d)=2cosa4(cos3d+cos2d+cosd),
∴由 若
f(an)=7π,∴f(an)=f(a1)+f(a2)+…+f(a7)=7π,
得14a4-2cosa4(cos3d+cos2d+cosd)=7π,
∴必有14a4=7π,且cosa4=0,
故a4=
,
∵公差d=
,
∴a1=
,a7=
,
∴f(a4)=2×
-cos
=π,有a1a7=
×
=
,则
=
,∴④正确.
故答案为:①③④
②若F(x)=f(x+a)-f(a),则F(-x)+F(x)=f(x+a)-f(a)+f(-x+a)-f(a)=f(a-x)+f(a+x)-2f(a),
∵f(x)在R上的“中心点”为(a,f(a)),
∴f(a-x)+f(a+x)=2f(a),
即F(-x)+F(x)=f(a-x)+f(a+x)-2f(a)=0,
∴F(-x)=-F(x),∴函数F(x)=f(x+a)-f(a)为R上的奇函数,∴②错误.
③函数f(x)=x3-3x2+6x-2,∴f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,
∴点(1,2)为函数f(x)的“中心点”,③正确;
④f(x)=2x-cosx,
∴f(a1)+f(a2)+…+f(a7)=2(a1+a2+…+a7)-(cosa1+cosa2+…+cosa7),
∵{an}是公差d=
| π |
| 8 |
∴a1+a2+…+a7=7a4,
cosa1+cosa2+…+cosa7=cos(a4-3d)+cos(a4-2d)+(cos(a4-d)+cosd+cos(a4+d)+cos(a4+2d)+cos(a4+3d)=2cosa4(cos3d+cos2d+cosd),
∴由 若
| 7 |
 |
| n=1 |
得14a4-2cosa4(cos3d+cos2d+cosd)=7π,
∴必有14a4=7π,且cosa4=0,
故a4=
| π |
| 2 |
∵公差d=
| π |
| 8 |
∴a1=
| π |
| 8 |
| 7π |
| 8 |
∴f(a4)=2×
| π |
| 2 |
| π |
| 2 |
| π |
| 8 |
| 7π |
| 8 |
| 7π2 |
| 64 |
| [f(a4)]2 |
| a1•a7 |
| 64 |
| 7 |
故答案为:①③④
点评:本题主要考查函数中心的定义的应用,综合性较强,运算量量较大,难度非常大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若(1-x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a1 十a2 十a3十a4十a5的值等于( )
| A、-31 | B、0 | C、1 | D、32 |
甲乙两名同学参加某项技能比赛,7名裁判给两人打出的分数如下茎叶图所示,依此判断( )

| A、甲成绩稳定且平均成绩较高 |
| B、乙成绩稳定且平均成绩较高 |
| C、甲成绩稳定,乙平均成绩较高 |
| D、乙成绩稳定,甲平均成绩较高 |
若tanα=2,则
等于( )
| sinα+cosα |
| sinα-cosα |
| A、-3 | ||
B、-
| ||
C、
| ||
| D、3 |
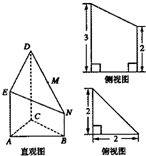 如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.