题目内容
求函数y=tan2x-2tanx-3,当x∈[-
,
]时的值域.
| π |
| 3 |
| π |
| 4 |
考点:三角函数的最值
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:令tanx=t,由x∈[-
,
],则-
≤t≤1,即有y=t2-2t-3=(t-1)2-4,由对称轴和区间的关系,可得y在[-
,1]上递减,即可求得值域.
| π |
| 3 |
| π |
| 4 |
| 3 |
| 3 |
解答:
解:令tanx=t,
由x∈[-
,
],则-
≤t≤1,
即有y=t2-2t-3=(t-1)2-4,
则y在[-
,1]上递减,
即有y的最小值为-4,最大值为2
.
则值域为[-4,2
].
由x∈[-
| π |
| 3 |
| π |
| 4 |
| 3 |
即有y=t2-2t-3=(t-1)2-4,
则y在[-
| 3 |
即有y的最小值为-4,最大值为2
| 3 |
则值域为[-4,2
| 3 |
点评:本题考查正切函数的单调性的运用,主要考查二次函数的值域问题,注意对称轴和区间的关系,属于基础题.

练习册系列答案
相关题目
设函数f(x)=|lnx|-
的两个零点为x1,x2,则有( )
| 1 |
| x+1 |
| A、x1x2<1 | ||
| B、x1x2=1 | ||
C、1<x1x2<
| ||
D、x1x2≥
|
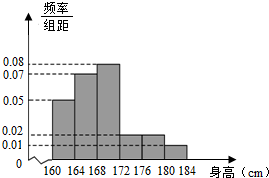 贵州省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
贵州省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.