题目内容
某班在5个男生和4个女生中选四人参加演讲比赛,选中的4人中有男有女,且男生甲和女生乙最少选中1个,则有多少种不同的选法?
考点:计数原理的应用
专题:排列组合
分析:分三大类,第一类,选男生甲也选女生乙,第二类,选男生甲不选女生乙,第三类,不选男生甲选女生乙,类中再继续进行分类,问题得以解决.
解答:
解:第一类,选男生甲也选女生乙,有
=21种,
第二类,选男生甲不选女生乙,1女3男,有C31C42=18种,2女2男,有C32C41=12种,3女1男,有C33=1种,共有18+12+1=31种,
第三类,不选男生甲选女生乙,1女3男,有C43=4种,2女2男,有C31C42=18种,3女1男,有C32C41=12种,共有4+18+12=34种,
根据分类计数原理,共有21+31+34=86种.
| C | 2 7 |
第二类,选男生甲不选女生乙,1女3男,有C31C42=18种,2女2男,有C32C41=12种,3女1男,有C33=1种,共有18+12+1=31种,
第三类,不选男生甲选女生乙,1女3男,有C43=4种,2女2男,有C31C42=18种,3女1男,有C32C41=12种,共有4+18+12=34种,
根据分类计数原理,共有21+31+34=86种.
点评:本题考查分类计数原理,关键是如何分类,本题是类中有类,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
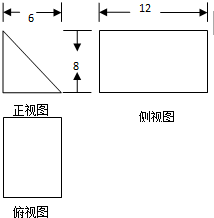 已知一块大理石表示的几何体的三视图如图所示,将该大理石切削、打磨加工成球体,则能得到的最大球体的体积为( )
已知一块大理石表示的几何体的三视图如图所示,将该大理石切削、打磨加工成球体,则能得到的最大球体的体积为( )A、
| ||
B、
| ||
| C、36π | ||
D、
|
已知A,B是以O为圆心的单位圆上的动点,且|
|=
,则
•
=( )
| AB |
| 2 |
| OB |
| AB |
| A、-1 | ||||
| B、1 | ||||
C、-
| ||||
D、
|
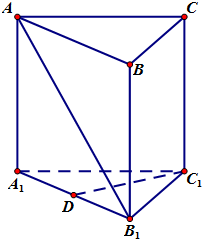 如图,直三棱柱ABC-A1B1C1中,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC=BC=| 2 |
| 3 |
(1)求证:C1D⊥AB1;
(2)若点F是BB1上的动点,求FB1的长度,使AB1⊥面C1DF.
sin
cos
tan
的值为( )
| 7π |
| 6 |
| 2π |
| 3 |
| 5π |
| 4 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|

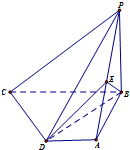 在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥BD,异面直线PA,CD所成角等于60°
在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥BD,异面直线PA,CD所成角等于60°