题目内容
16.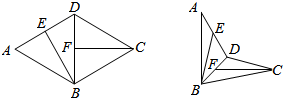 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )| A. | ($\frac{π}{6}$,$\frac{π}{3}$) | B. | ($\frac{π}{6}$,$\frac{π}{2}$] | C. | ($\frac{π}{3}$,$\frac{π}{2}$] | D. | ($\frac{π}{3}$,$\frac{2π}{3}$) |
分析 可设菱形的边长为1,从而由条件可得到BE=CF=$\frac{\sqrt{3}}{2}$,BD=1,根据向量加法的平行四边形法则及向量减法的几何意义可得到$\overrightarrow{BE}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BD}),\overrightarrow{CF}=\frac{1}{2}(\overrightarrow{BD}-2\overrightarrow{BC})$,然后进行向量数量积的运算可求出$\overrightarrow{BE}•\overrightarrow{CF}$,从而可得到$cos<\overrightarrow{BE},\overrightarrow{CF}>=\frac{\frac{1}{8}-\frac{1}{2}cos<\overrightarrow{BA},\overrightarrow{BC}>}{\frac{3}{4}}$,而由$-\frac{1}{2}<cos<\overrightarrow{BA},\overrightarrow{BC}><1$可得$-\frac{1}{2}<cos<\overrightarrow{BE},\overrightarrow{CF}><\frac{1}{2}$,从而可以得到向量$\overrightarrow{BE},\overrightarrow{CF}$夹角的范围,进而便可得出异面直线BE与CF所成角的取值范围.
解答 解:可设菱形的边长为1,则BE=CF=$\frac{\sqrt{3}}{2}$,BD=1;
线段AD,BD的中点分别为E,F;
∴$\overrightarrow{BE}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BD})$,$\overrightarrow{CF}=\frac{1}{2}(\overrightarrow{CB}+\overrightarrow{CD})$=$\frac{1}{2}(\overrightarrow{BD}-2\overrightarrow{BC})$;
∴$\overrightarrow{BE}•\overrightarrow{CF}=\frac{1}{4}(\overrightarrow{BA}+\overrightarrow{BD})•(\overrightarrow{BD}-2\overrightarrow{BC})$=$\frac{1}{4}\overrightarrow{BA}•\overrightarrow{BD}-\frac{1}{2}\overrightarrow{BA}•\overrightarrow{BC}+\frac{1}{4}{\overrightarrow{BD}}^{2}-\frac{1}{2}$$\overrightarrow{BD}•\overrightarrow{BC}$
=$\frac{1}{8}-\frac{1}{2}cos<\overrightarrow{BA},\overrightarrow{BC}>+\frac{1}{4}-\frac{1}{4}$=$\frac{1}{8}-\frac{1}{2}cos<\overrightarrow{BA},\overrightarrow{BC}>$;
∴$cos<\overrightarrow{BE},\overrightarrow{CF}>=\frac{\overrightarrow{BE}•\overrightarrow{CF}}{|\overrightarrow{BE}||\overrightarrow{CF}|}$=$\frac{\frac{1}{8}-\frac{1}{2}cos<\overrightarrow{BA},\overrightarrow{BC}>}{\frac{3}{4}}$;
由图看出$-\frac{1}{2}<cos<\overrightarrow{BA},\overrightarrow{BC}><1$;
∴$-\frac{1}{2}<cos<\overrightarrow{BE},\overrightarrow{CF}><\frac{1}{2}$;
∴$\frac{π}{3}<<\overrightarrow{BE},\overrightarrow{CF}><\frac{2π}{3}$;
即异面直线BE与CF所成角的取值范围是$(\frac{π}{3},\frac{π}{2}]$.
故选:C.
点评 考查向量加法的平行四边形法则,向量减法的几何意义,以及向量数量积的运算及其计算公式,向量夹角余弦的计算公式,清楚向量夹角的范围,以及异面直线所成角的范围.

| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (3,0) | B. | (-3,0) | C. | (0,3) | D. | (0,-3) |
 如图,点O为作简谐振动的物体的平衡位置,取向右方向为正方向,若振幅为3cm,周期为4s,且物体向右运动到距平衡位置最远处时开始计时.则该物体10s时刻的路程为-3cm.
如图,点O为作简谐振动的物体的平衡位置,取向右方向为正方向,若振幅为3cm,周期为4s,且物体向右运动到距平衡位置最远处时开始计时.则该物体10s时刻的路程为-3cm.