题目内容
5．抛物线的标准方程是y2=-12x，则其焦点坐标是（ ）| A． | （3，0） | B． | （-3，0） | C． | （0，3） | D． | （0，-3） |
分析 利用抛物线的标准方程求解即可．
解答 解：抛物线的标准方程是y2=-12x，可知焦点坐标在x轴上，P=6，
焦点坐标（-3，0）．
故选：B．
点评 本题考查抛物线的简单性质的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
16．
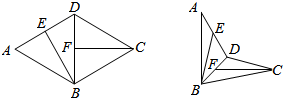如图，在菱形ABCD中，∠BAD=60°，线段AD，BD的中点分别为E，F．现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是（ ）
如图，在菱形ABCD中，∠BAD=60°，线段AD，BD的中点分别为E，F．现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是（ ）| A． | （$\frac{π}{6}$，$\frac{π}{3}$） | B． | （$\frac{π}{6}$，$\frac{π}{2}$] | C． | （$\frac{π}{3}$，$\frac{π}{2}$] | D． | （$\frac{π}{3}$，$\frac{2π}{3}$） |
20．函数y=2sin（3x+$\frac{π}{6}$），x∈R的最小正周期是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{3π}{2}$ | D． | π |
10．将函数y=cos2x的图象向左平移$\frac{π}{3}$个单位长度，所得图象的函数解析式为（ ）
| A． | $y=cos（2x-\frac{2π}{3}）$ | B． | $y=cos（2x+\frac{π}{3}）$ | C． | $y=cos（2x+\frac{2π}{3}）$ | D． | $y=cos（2x-\frac{π}{3}）$ |