题目内容
6.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则目标函数z=x+6y的最大值为18.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合的得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$作出可行域如图,
A(0,3),
化目标函数z=x+6y为y=-$\frac{x}{6}+\frac{z}{6}$,
由图可知,当直线y=-$\frac{x}{6}+\frac{z}{6}$过A时,直线在y轴上的截距最大,z有最大值为18.
故答案为:18.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
16.已知函数f(x)的义域为D.对于任意的x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x_1})•f({x_2})}=M$成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
11.函数$f(x)=-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x$的极大值点是( )
| A. | $-\frac{4}{5}$ | B. | 1 | C. | $\frac{7}{6}$ | D. | -2 |
18.某研究机构对高二学生的记忆力x和判断力y进行统计分析,得下表数据
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)试根据(1)求出的线性回归方程,预测记忆力为9的同学的判断力.
($\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
| x | 6 | 8 | 10 | 12 |
| y | 3 | 4 | 6 | 7 |
(2)试根据(1)求出的线性回归方程,预测记忆力为9的同学的判断力.
($\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
16.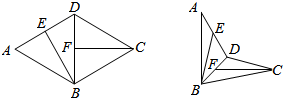 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )| A. | ($\frac{π}{6}$,$\frac{π}{3}$) | B. | ($\frac{π}{6}$,$\frac{π}{2}$] | C. | ($\frac{π}{3}$,$\frac{π}{2}$] | D. | ($\frac{π}{3}$,$\frac{2π}{3}$) |
