题目内容
1.已知函数f(x)=2sinxcosx,x∈R.(Ⅰ)求f($\frac{π}{4}$)的值;
(Ⅱ)求函数f(x)的最小正周期;
(Ⅲ)求函数g(x)=f(x)+f(x+$\frac{π}{4}$)的最大值.
分析 (Ⅰ)利用特殊角的三角函数值即可计算得解.
(Ⅱ)利用三角函数周期公式即可计算得解.
(Ⅲ)由诱导公式,两角和的正弦函数公式化简可得解析式g(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),利用正弦函数的图象和性质即可得解.
解答 解:(Ⅰ)由题意得f($\frac{π}{4}$)=2sin$\frac{π}{4}$cos$\frac{π}{4}$=1,
(Ⅱ)∵f(x)=sin2x,
∴函数f(x)的最小正周期为T=$\frac{2π}{2}$=π,
(Ⅲ)∵g(x)=sin2x+sin(2x+$\frac{π}{2}$)=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
∴当x=k$π+\frac{π}{8}$,k∈Z时,函数g(x)的最大值为$\sqrt{2}$.
点评 本题主要考查了特殊角的三角函数值,三角函数周期公式,诱导公式,两角和的正弦函数公式的应用,考查了正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
11.函数$f(x)=-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x$的极大值点是( )
| A. | $-\frac{4}{5}$ | B. | 1 | C. | $\frac{7}{6}$ | D. | -2 |
9.设抛物线y2=2px(p>0)的焦点为F.若F到直线y=$\sqrt{3}$x的距离为$\sqrt{3}$,则p=( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
16.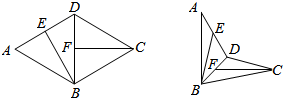 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )| A. | ($\frac{π}{6}$,$\frac{π}{3}$) | B. | ($\frac{π}{6}$,$\frac{π}{2}$] | C. | ($\frac{π}{3}$,$\frac{π}{2}$] | D. | ($\frac{π}{3}$,$\frac{2π}{3}$) |
10.将函数y=cos2x的图象向左平移$\frac{π}{3}$个单位长度,所得图象的函数解析式为( )
| A. | $y=cos(2x-\frac{2π}{3})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x+\frac{2π}{3})$ | D. | $y=cos(2x-\frac{π}{3})$ |
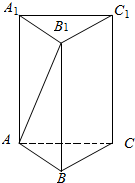 如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.
如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.