题目内容
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)求出曲线y=x2-2x-3与坐标轴的交点坐标,设出圆的一般方程,把点的坐标代入圆的一般方程列方程组求解系数,则答案可求;
(2)由点到直线的距离公式求出圆心到直线x+y+a=0的距离,利用弦心距、弦长与圆的半径之间的关系列式求解a的值.
(2)由点到直线的距离公式求出圆心到直线x+y+a=0的距离,利用弦心距、弦长与圆的半径之间的关系列式求解a的值.
解答:
解:(1)取x=0,得y=-3,曲线与y轴的交点是(0,-3).
令y=0,得x2-2x-3=0,解得x=-1或x=3,
即曲线与x轴的交点是(-1,0),(3,0).
设所求圆C的方程是x2+y2+Dx+Ey+F=0,
则
,解得:D=-2,E=2,F=-3.
∴圆C的方程是x2+y2-2x+2y-3=0;
(2)圆C的方程可化为(x-1)2+(y+1)2=(
)2,
∴圆心C(1,-1),半径r=
.
圆心C到直线x+y+a=0的距离d=
=
.
由于d2+(
AB)2=r2,
∴(
)2+12=(
)2,解得a=±2
.
令y=0,得x2-2x-3=0,解得x=-1或x=3,
即曲线与x轴的交点是(-1,0),(3,0).
设所求圆C的方程是x2+y2+Dx+Ey+F=0,
则
|
∴圆C的方程是x2+y2-2x+2y-3=0;
(2)圆C的方程可化为(x-1)2+(y+1)2=(
| 5 |
∴圆心C(1,-1),半径r=
| 5 |
圆心C到直线x+y+a=0的距离d=
| |1+(-1)+a| | ||
|
| |a| | ||
|
由于d2+(
| 1 |
| 2 |
∴(
| |a| | ||
|
| 5 |
| 2 |
点评:本题考查了圆的方程的求法,直线与圆的方程关系的应用,训练了点到直线的距离公式,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的体积是( )
A、
| ||||
B、
| ||||
C、2S
| ||||
D、S
|
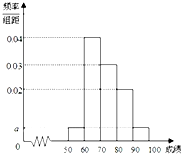 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 已知
已知 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.