题目内容
已知圆锥的底面半径为R,高为H,则圆锥内接圆柱体的体积最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:计算题
分析:画出圆锥的轴截面,设圆锥内接圆柱体的底面圆的半径为r,高为h,利用比例关系求出h,列出圆锥内接圆柱体的体积关于r的函数,利用基本不等式求最大值.
解答:
解:如图是圆锥的轴截面:
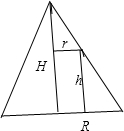
设圆锥内接圆柱体的底面圆的半径为r,高为h,
则
=
⇒h=(1-
)H,
V圆柱=πr2(1-
)H=π
×
×
×(2-
)H≤π×
H×(
)3=
πR2H.
当r=
R时,取“=”.
故选B.

设圆锥内接圆柱体的底面圆的半径为r,高为h,
则
| H-h |
| H |
| r |
| R |
| r |
| R |
V圆柱=πr2(1-
| r |
| R |
| R2 |
| 2 |
| r |
| R |
| r |
| R |
| 2r |
| R |
| R2 |
| 2 |
| 2 |
| 3 |
| 4 |
| 27 |
当r=
| 2 |
| 3 |
故选B.
点评:本题考查了圆锥的内接圆柱的最大体积问题,解答的关键是利用比例关系构造以r为自变量的函数,利用基本不等式求最值.

练习册系列答案
相关题目
函数f(x)由下表定义:
若a1=2,an+1=f(an),n=l,2,3,…,则数列{an}的前2010项的和S2010=( )
| x | 1 | 2 | 3 | 4 | 5 |
| F(x) | 4 | 1 | 3 | 5 | 2 |
| A、6021 | B、6023 |
| C、6025 | D、6027 |
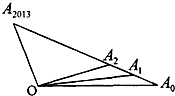 如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,
如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,| OA0 |
| a |
| OA2013 |
| b |
| a |
| b |
| OA0 |
| OA1 |
| OA2 |
| OA2013 |
A、1006(
| ||||
B、1007(
| ||||
C、2012(
| ||||
D、2014(
|
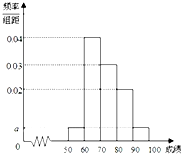 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].