题目内容
6．第96届（春季）全国糖酒商品交易会于2017年3月23日至25日在四川举办．展馆附近一家川菜特色餐厅为了研究参会人数与本店所需原材料数量的关系，在交易会前查阅了最近5次交易会的参会人数x（万人）与餐厅所用原材料数量y（袋），得到如下数据：| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x（万人） | 11 | 9 | 8 | 10 | 12 |
| 原材料t（袋） | 28 | 23 | 20 | 25 | 29 |
（Ⅱ）若该店现有原材料12袋，据悉本次交易会大约有13万人参加，为了保证原材料能够满足需要，则该店应至少再补充原材料多少袋？
（参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$））
分析 （Ⅰ）根据表中数据求出$\overline{x}$，$\overline{y}$，即可求出$\stackrel{∧}{b}$，在求出$\stackrel{∧}{a}$，可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
（Ⅱ）由（Ⅰ）的线性回归方程，当x=12时，求出$\stackrel{∧}{y}$，减去12可得补充原材料的袋数．
解答 解：（Ⅰ）根据表中数据可得$\overline{x}$=$\frac{11+9+8+10+12}{5}=10$，$\overline{y}$=$\frac{28+23+20+25+29}{5}=25$．
则：$\sum_{i=1}^{5}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）$=（1×3）+（-1）×（-2）+（-2）×（-5）+0+2×4=23．
$\sum_{i=1}^{5}（{x}_{i}-\overline{x}）^{2}$=1+（-1）2+（-2）2+0+22=10
由公式，得$\stackrel{∧}{b}$=2.3．
线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，代入可得$\stackrel{∧}{a}$=2．
∴y关于x的线性回归方程为：$\stackrel{∧}{y}$=2.3x+2．
（Ⅱ）由题意，当x=12时，可得出$\stackrel{∧}{y}$=31.9
故而31.9-12=19.9≈20袋．
所以，该店应至少再补充原材料20袋．
点评 本题考查线性回归方程的求法，考查最小二乘法，属于基础题
练习册系列答案
相关题目
17．已知随机变量X服从正态分布N（3，1），且P（X≥4）=0.1587，则P（2＜X＜4）=（ ）
| A． | 0.6826 | B． | 0.3413 | C． | 0.4603 | D． | 0.9207 |
14．已知直线PA，PB分别与半径为1的圆O相切于点A，B，PO=2，$\overrightarrow{PM}=2λ\overrightarrow{PA}+（1-λ）\overrightarrow{PB}$．若点M在圆O的内部（不包括边界），则实数λ的取值范围是（ ）
| A． | （-1，1） | B． | $（0，\frac{2}{3}）$ | C． | $（\frac{1}{3}，1）$ | D． | （0，1） |
1．
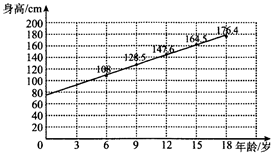某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况，随机抽取6岁，9岁，12岁，15岁，18岁的青少年身高数据各1000个，根据各年龄段平均身高作出如图所示的散点图和回归直线L．根据图中数据，下列对该样本描述错误的是（ ）
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况，随机抽取6岁，9岁，12岁，15岁，18岁的青少年身高数据各1000个，根据各年龄段平均身高作出如图所示的散点图和回归直线L．根据图中数据，下列对该样本描述错误的是（ ）| A． | 据样本数据估计，该地区青少年身高与年龄成正相关 | |
| B． | 所抽取数据中，5000名青少年平均身高约为145cm | |
| C． | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D． | 从这5种年龄的青少年中各取一人的身高数据，由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |
11．
某公司为了准确地把握市场，做好产品生产计划，对过去四年的数据进行整理得到了第x年与年销量y（单位：万件）之间的关系如表：
（Ⅰ）在图中画出表中数据的散点图；
（Ⅱ）根据（Ⅰ）中的散点图拟合y与x的回归模型，并用相关系数加以说明；
（Ⅲ）建立y关于x的回归方程，预测第5年的销售量约为多少？．
附注：参考数据：$\sqrt{\sum_{i=1}^4{{{（{y_i}-\overline y）}^2}}}≈32.6$，$\sqrt{5}≈2.24$，$\sum_{i=1}^4{{x_i}{y_i}=418}$．
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}\sum_{i=1}^n{{{（{y_i}-\overline y）}^2}}}}}$，
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
某公司为了准确地把握市场，做好产品生产计划，对过去四年的数据进行整理得到了第x年与年销量y（单位：万件）之间的关系如表：| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
（Ⅱ）根据（Ⅰ）中的散点图拟合y与x的回归模型，并用相关系数加以说明；
（Ⅲ）建立y关于x的回归方程，预测第5年的销售量约为多少？．
附注：参考数据：$\sqrt{\sum_{i=1}^4{{{（{y_i}-\overline y）}^2}}}≈32.6$，$\sqrt{5}≈2.24$，$\sum_{i=1}^4{{x_i}{y_i}=418}$．
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}\sum_{i=1}^n{{{（{y_i}-\overline y）}^2}}}}}$，
回归方程$\widehaty=\widehata+\widehatbx$中斜率和截距的最小二乘法估计公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．