Question

13．直三棱柱ABC-A₁B₁C₁的所有顶点均在同一个球面上，且AB=AC=3，∠BAC=60°，AA₁=2．则该球的体积为$\frac{32π}{3}$．

Answer 1

分析 由题意知：△ABC为等边三角形，设其中心为O，设球心为O₁，则△AO₁O为直角三角形，AO⊥OO₁，由此能求出球的半径，从而能求出该球的体积．

解答 解：由题意知：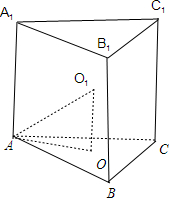
△ABC为等边三角形，设其中心为O，
则AO=BO=CO=$\sqrt{3}$，
设球心为O₁，则△AO₁O为直角三角形，AO⊥OO₁，
∴球的半径r=$\sqrt{（\sqrt{3}）^{2}+{1}^{2}}$=2，
∴该球的体积为V_球=$\frac{4}{3}π×{2}^{3}$=$\frac{32π}{3}$．
故答案为：$\frac{32π}{3}$．

点评 本题考查球的体积的求法，考查直三棱柱、球等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想，是中档题．