题目内容
已知向量
=(-1,
),
=(cosx,sinx),f(x)=
•
(Ⅰ)若cosθ=
,0<θ<
,求f(θ);
(Ⅱ)若1≤f(θ)≤
,θ∈[0,π],求θ的取范围;
(Ⅲ)在条件(Ⅱ)下,求函数F(θ)=
的值域.
| m |
| 3 |
| n |
| m |
| n |
(Ⅰ)若cosθ=
| 3 |
| 5 |
| π |
| 2 |
(Ⅱ)若1≤f(θ)≤
| 3 |
(Ⅲ)在条件(Ⅱ)下,求函数F(θ)=
| f(θ) | ||
f(
|
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(Ⅰ)先根据题意求得函数解析式,根据cosθ的值求得sinθ代入函数解析式.
(Ⅱ)利用两角和公式对函数解析式化简,进而根据f(θ)的范围确定sin(θ-
)进而确定θ的范围.
(Ⅲ)根据f(θ)的表达式对数F(θ)进而化简,根据θ的范围确定tan(θ-
)的范围,进而确定F(θ)的范围.
(Ⅱ)利用两角和公式对函数解析式化简,进而根据f(θ)的范围确定sin(θ-
| π |
| 6 |
(Ⅲ)根据f(θ)的表达式对数F(θ)进而化简,根据θ的范围确定tan(θ-
| π |
| 6 |
解答:
解:(Ⅰ)f(x)=
•
=-cosx+
sinx,
∵cosθ=
,0<θ<
,
∴sinθ=
,
∴f(θ)=-
+
×
=
.
(Ⅱ)f(x)=-cosx+
sinx=2sin(x-
),
∵1≤f(θ)≤
,
∴1≤2sin(θ-
)≤
,
∴
≤sin(θ-
)≤
,
∵θ∈[0,π],
∴θ-
∈[-
,
],
∴
≤θ-
≤
或
≤θ-
≤
,
∴
≤θ≤
或
≤θ≤π.
(Ⅲ)F(θ)=
=
=
=tan(θ-
),
由(Ⅱ)知,
≤θ≤
或
≤θ≤π,
∴
≤tan(θ-
)≤
或-
≤tan(θ-
)≤-
.
即F(θ)的值域是[
,
]∪[-
,-
].
| m |
| n |
| 3 |
∵cosθ=
| 3 |
| 5 |
| π |
| 2 |
∴sinθ=
| 4 |
| 5 |
∴f(θ)=-
| 3 |
| 5 |
| 3 |
| 4 |
| 5 |
4
| ||
| 5 |
(Ⅱ)f(x)=-cosx+
| 3 |
| π |
| 6 |
∵1≤f(θ)≤
| 3 |
∴1≤2sin(θ-
| π |
| 6 |
| 3 |
∴
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
∵θ∈[0,π],
∴θ-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
(Ⅲ)F(θ)=
| f(θ) | ||
f(
|
2sin(θ-
| ||||
2sin(
|
sin(θ-
| ||
cos(θ-
|
| π |
| 6 |
由(Ⅱ)知,
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
∴
| ||
| 3 |
| π |
| 6 |
| 3 |
| 3 |
| π |
| 6 |
| ||
| 3 |
即F(θ)的值域是[
| ||
| 3 |
| 3 |
| 3 |
| ||
| 3 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.综合考查了学生推理和运算的能力.

练习册系列答案
相关题目
函数y=ln(3x-2)上过点(1,0)的切线方程( )
| A、y=x-1 |
| B、y=3x-3 |
| C、y=-x-1 |
| D、y=3x+1 |
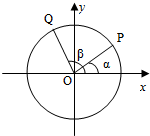 如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(
如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(