题目内容
已知关于x的不等式ax2-3x+2≤0的解集为{x|1≤x≤b}.
(1)求实数a,b的值;
(2)解关于x的不等式:
>0(c为常数).
(1)求实数a,b的值;
(2)解关于x的不等式:
| x-c |
| ax-b |
考点:一元二次不等式的解法
专题:计算题,不等式的解法及应用
分析:(1)由题意知1,b为关于x的方程ax2-3x+2=0的两根,由韦达定理可得方程组,解出即可;
(2)不等式等价于(x-c)(x-2)>0,按照对应方程的根2、c的大小关系分三种情况讨论可得;
(2)不等式等价于(x-c)(x-2)>0,按照对应方程的根2、c的大小关系分三种情况讨论可得;
解答:
解:(1)由题意知1,b为关于x的方程ax2-3x+2=0的两根,
则
,∴a=1,b=2.
(2)不等式等价于(x-c)(x-2)>0,
所以:当c>2时解集为{x|x>c或x<2};
当c=2时解集为{x|x≠2,x∈R};
当c<2时解集为{x|x>2或x<c}.
则
|
(2)不等式等价于(x-c)(x-2)>0,
所以:当c>2时解集为{x|x>c或x<2};
当c=2时解集为{x|x≠2,x∈R};
当c<2时解集为{x|x>2或x<c}.
点评:该题考查一元二次不等式的解法,属基础题,深刻理解“三个二次”间的关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
要得到函数y=cos(2x-
)的图象,可由函数y=cos2x( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 (文) 已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.
(文) 已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.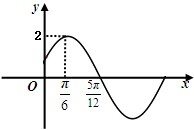 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<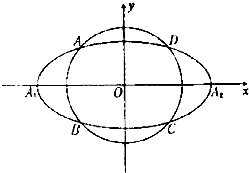 如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2:
如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2: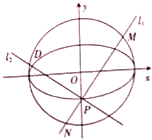 已知椭圆E:
已知椭圆E: