题目内容
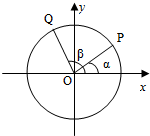 如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(
如图,以Ox为始边分别作角α与β(0<α<β<π),它们的终边分别与单位圆相交于点P、Q,已知点P的坐标为(| 3 |
| 5 |
| 4 |
| 5 |
(1)求sin2α的值;
(2)若β-α=
| π |
| 2 |
考点:单位圆与周期性
专题:三角函数的求值
分析:(1)由三角函数的定义,得出cosα、sinα,从而求出sin2α的值;
(2)由β-α=
,求出sinβ,cosβ的值,从而求出cos(α+β)的值.
(2)由β-α=
| π |
| 2 |
解答:
解:(1)由三角函数的定义得,
cosα=
,sinα=
;
∴sin2α=2sinαcosα=2×
×
=
;
(2)∵β-α=
,
∴sinβ=sin(
+α)=cosα=
.
cosβ=cos(
+α)=-sinα=-
,
∴cos(α+β)=cosαcosβ-sinαsinβ=
×(-
)-
×
=-
.
cosα=
| 3 |
| 5 |
| 4 |
| 5 |
∴sin2α=2sinαcosα=2×
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
(2)∵β-α=
| π |
| 2 |
∴sinβ=sin(
| π |
| 2 |
| 3 |
| 5 |
cosβ=cos(
| π |
| 2 |
| 4 |
| 5 |
∴cos(α+β)=cosαcosβ-sinαsinβ=
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
点评:本题考查了三角函数的求值与应用问题,解题时应根据三角函数的定义以及三角恒等公式进行计算,是基础题.

练习册系列答案
相关题目
某单位随机统计了某4天的用电量(度)与当天气温(℃)如下表,以了解二者的关系.
由表中数据得回归直线方程y=-2x+a,则a=( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
| A、60 | B、58 |
| C、40 | D、以上都不对 |
 如图,在山底测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得山顶仰角为75°,求山高BC.
如图,在山底测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得山顶仰角为75°,求山高BC.