题目内容
已知条件p：x=2，条件q：（x-2）（x-3）=0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：当p成立时，将x=2，代入q，显然成立，故前者是后者的充分条件，反之不一定成立，由此可得结论．
解答：
解：若x=2成立，则（x-2）（x-3）=0显然成立，故p是q的充分条件；
反之，若（x-2）（x-3）=0，则x=2或x=3，则p未必成立．
故p是q的充分不必要条件．
故选A
反之，若（x-2）（x-3）=0，则x=2或x=3，则p未必成立．
故p是q的充分不必要条件．
故选A
点评：本题考查了条件的充分性、必要性的判断方法，一般是双向推理下结论．
练习册系列答案
相关题目
已知幂函数f（x）=（m2-3m+3）•xm+1为偶函数，则m=（ ）
| A、1 | B、2 | C、1或2 | D、3 |
函数f（x）=（x2-2x-3）（x2-2x-5）的值域是（ ）
| A、（-∞，-1] |
| B、[-1，+∞） |
| C、[24，+∞） |
| D、（24，+∞） |
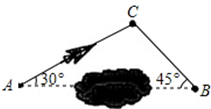一架飞机从马来西亚吉隆坡飞往中国北京，两地相距4500km．飞行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿与原来的飞行方向成30°角的方向飞行，飞行到途中，再沿与原来的飞行方向成45°角的方向继续飞行直到终点．这样飞机的飞行路程比原来的路程4500km远了多少？（参考数据：