题目内容
已知命题p：?x∈[2，3]，x2-a≥0，命题q：方程
+
=1表示双曲线方程，若￢p为真，p或q为真，求实数a的取值范围．
| x2 |
| 3 |
| y2 |
| a-7 |
考点：复合命题的真假
专题：计算题
分析：分别判定命题p，q为真命题时的等价条件，然后利用p或q为真命题，p且q为假命题，则p、q一真一假，确定m的取值范围．
解答：
解：
若命题p为真命题，
则a≤x2，x∈[2，3]时恒成立
所以a≤4
若命题q为真命题
则有a-7＜0
解得a＜7
∵￢p为真，p或q为真
∴p假q真
∴
故实数a的取值范围为（4，7）
若命题p为真命题，
则a≤x2，x∈[2，3]时恒成立
所以a≤4
若命题q为真命题
则有a-7＜0
解得a＜7
∵￢p为真，p或q为真
∴p假q真
∴
|
故实数a的取值范围为（4，7）
点评：本题主要考查命题真假的应用，要求熟练掌握复合命题的真值表，解答本题的关键是正确理解命题P的含义并求出命题P为真时m的范围．
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=n2-n+1，则其通项an=（ ）
| A、2n-1 | |||||
| B、2n-2 | |||||
C、
| |||||
| D、n2-n+1 |
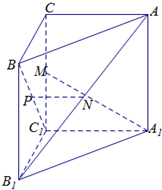如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，且∠ACB=90°，∠BAC=30°，BC=1，AA1=
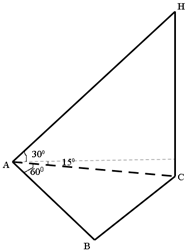某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处进行该仪器的垂直弹射，观察点A、B两地相距100米，∠BAC=60°，其中A到C的距离比B到C的距离远40米．A地测得该仪器在C处的俯角为15°，A地测得最高点H的仰角为30°，求该仪器的垂直弹射高度CH．（结果保留根式）
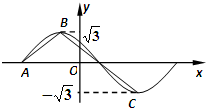函数f（x）=