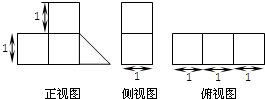
题目内容
已知函数f(x)=alnx-x+1,a∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)≤0在x∈(0,+∞)上恒成立,求所有实数a的值;
(Ⅲ)对任意的0<m<n,证明:
-1<
<
-1.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)≤0在x∈(0,+∞)上恒成立,求所有实数a的值;
(Ⅲ)对任意的0<m<n,证明:
| 1 |
| n |
| f(n)-f(m) |
| n-m |
| 1 |
| m |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:对于第一问可通过对函数求导求单调区间,再讨论a的范围确定导函数的符号,从而求出单调区间.
对于第二问分别讨论a≤0和a>0的情况:a≤0时,发现在(0,1)上函数f(x)>0,∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立;
当a>0时,再次求导求出a的值.
对于第三问是在第二问的基础上得到关系式:lnx≤x-1和-lnx≥1-x,通过代入求值,替换的方法结论得证.
对于第二问分别讨论a≤0和a>0的情况:a≤0时,发现在(0,1)上函数f(x)>0,∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立;
当a>0时,再次求导求出a的值.
对于第三问是在第二问的基础上得到关系式:lnx≤x-1和-lnx≥1-x,通过代入求值,替换的方法结论得证.
解答:
解:(1)f′(x)=
-1=
(x>0),
当a≤0时,f'(x)<0,f(x)减区间为(0,+∞),
当a>0时,由f'(x)>0得0<x<a,由f'(x)<0得x>a;
∴f(x)递增区间为(0,a),递减区间为(a,+∞).
(2)由(1)知:当a≤0时,f(x)在(0,+∞)上为减区间,而f(1)=0,
∴在(0,1)上函数f(x)>0,
∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立; (
当a>0时,f(x)在(0,a)上递增,在(a,+∞)上递减,f(x)max=f(a)=alna-a+1,令g(a)=alna-a+1,
依题意有g(a)≤0,而g'(a)=lna,且a>0
∴g(a)在(0,1)上递减,在(1,+∞)上递增,
∴g(a)min=g(1)=0,故a=1(19分)
(3)由(2)知:a=1时,f(x)=lnx-x+1且f(x)≤0恒成立
即lnx≤x-1恒成立
则
=
=
-1≤
-1≤
-1
又由lnx≤x-1知-lnx≥1-x在(0,+∞)上恒成立
∴
=
-1=
-1≥
-1=
-1
综上所述:对任意的0<m<n,证明:
-1<
<
-1
| a |
| x |
| a-x |
| x |
当a≤0时,f'(x)<0,f(x)减区间为(0,+∞),
当a>0时,由f'(x)>0得0<x<a,由f'(x)<0得x>a;
∴f(x)递增区间为(0,a),递减区间为(a,+∞).
(2)由(1)知:当a≤0时,f(x)在(0,+∞)上为减区间,而f(1)=0,
∴在(0,1)上函数f(x)>0,
∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立; (
当a>0时,f(x)在(0,a)上递增,在(a,+∞)上递减,f(x)max=f(a)=alna-a+1,令g(a)=alna-a+1,
依题意有g(a)≤0,而g'(a)=lna,且a>0
∴g(a)在(0,1)上递减,在(1,+∞)上递增,
∴g(a)min=g(1)=0,故a=1(19分)
(3)由(2)知:a=1时,f(x)=lnx-x+1且f(x)≤0恒成立
即lnx≤x-1恒成立
则
| f(n)-f(m) |
| n-m |
| (lnn-n+1)-(lnm-m+1) |
| n-m |
ln
| ||
| n-m |
| ||
| n-m |
| 1 |
| m |
又由lnx≤x-1知-lnx≥1-x在(0,+∞)上恒成立
∴
| f(n)-f(m) |
| n-m |
ln
| ||
| n-m |
-ln
| ||
| n-m |
1-
| ||
| n-m |
| 1 |
| n |
综上所述:对任意的0<m<n,证明:
| 1 |
| n |
| f(n)-f(m) |
| n-m |
| 1 |
| m |
点评:本题是一道综合题,函数求导,利用导数求单调区间,求函数极值问题,考察了不等式的证明以及各知识点的综合应用.

练习册系列答案
相关题目
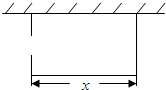 某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.