题目内容
已知正项数列{xn}满足xn+
<2(n∈N*).
(1)证明:xn+
≥2;
(2)证明:xn<xn+1;
(3)证明:
<xn<
.
| 1 |
| xn+1 |
(1)证明:xn+
| 1 |
| xn |
(2)证明:xn<xn+1;
(3)证明:
| n-1 |
| n |
| n+1 |
| n |
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)可以利用基本不等式进行证明;(2)利用(1)的结论,通过不等式传递,得到本题结果;(3)可以将原不等式折成两个不等式,再利用数学归纳法、反证法分别进行证明.
解答:
证明:(1)方法一:因为xn>0,所以xn+
≥2
=2,
故xn+
≥2,当且仅当xn=1时,等号成立.
方法二:因为xn>0,所以xn+
-2=(
-
)2≥0,
故xn+
≥2,当且仅当xn=1时,等号成立.
(2)由(1)知xn+
≥2,又xn+
<2,
所以
>
,所以xn<xn+1.
(3)先证:xn>
(数学归纳法)
当n=1时,不等式显然成立;
假设当n=k(k∈N*)时不等式成立,即xk>
.
当n=k+1时,由xn+
<2得xk+1>
>
=
,
即当n=k+1时,不等式成立;
综上,对一切n∈N*都有xn>
成立.
再证:xn<
由xn>0及xn+
<2(n∈N*),得xn<2(n∈N*),
所以当n=1时,不等式显然成立;
当n≥2时,证明xn<
(反证法)
假设存在k,使得xk≥
,
则有xk+1>
≥
=
,即xk+1>
,
所以xk+2>
,xk+3>
,┅,x2k-2>
,x2k-1>2,
与题设x2k-1+
<2矛盾.
所以对一切n∈N*都有xn<
成立.
所以对一切n∈N*都有
<xn<
成立.
| 1 |
| xn |
xn×
|
故xn+
| 1 |
| xn |
方法二:因为xn>0,所以xn+
| 1 |
| xn |
| xn |
| 1 | ||
|
故xn+
| 1 |
| xn |
(2)由(1)知xn+
| 1 |
| xn |
| 1 |
| xn+1 |
所以
| 1 |
| xn |
| 1 |
| xn+1 |
(3)先证:xn>
| n-1 |
| n |
当n=1时,不等式显然成立;
假设当n=k(k∈N*)时不等式成立,即xk>
| k-1 |
| k |
当n=k+1时,由xn+
| 1 |
| xn+1 |
| 1 |
| 2-xk |
| 1 | ||
2-
|
| k |
| k+1 |
即当n=k+1时,不等式成立;
综上,对一切n∈N*都有xn>
| n-1 |
| n |
再证:xn<
| n+1 |
| n |
由xn>0及xn+
| 1 |
| xn+1 |
所以当n=1时,不等式显然成立;
当n≥2时,证明xn<
| n+1 |
| n |
假设存在k,使得xk≥
| k+1 |
| k |
则有xk+1>
| 1 |
| 2-xk |
| 1 | ||
2-
|
| k |
| k-1 |
| k |
| k-1 |
所以xk+2>
| k-1 |
| k-2 |
| k-2 |
| k-3 |
| 3 |
| 2 |
与题设x2k-1+
| 1 |
| x2k |
所以对一切n∈N*都有xn<
| n+1 |
| n |
所以对一切n∈N*都有
| n-1 |
| n |
| n+1 |
| n |
点评:本题考查的不等式和数列的知识,包括基本不等式、解不等式、数列、数学归纳法、反证法,思维量较大,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数z=3-4i,则|z|=( )
| A、3 | B、4 | C、1 | D、5 |
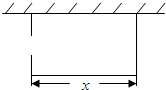 某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.