题目内容
已知两正数x,y满足x+y=1,求z=(x+
)(y+
)的最小值.
| 1 |
| x |
| 1 |
| y |
考点:基本不等式
专题:不等式的解法及应用
分析:将z进行变形构造出适合基本不等式适用的结构,再利用基本不等式求最值.
解答:
解:z=(x+
)(y+
)=xy+
+
+
=xy+
+
=xy+
-2,
令t=xy,则0<t=xy≤(
)2=
,(当且仅当x=y时取等号).
由f(t)=t+
在(0,
]上单调递减,故当t=
时,f(t)=t+
有最小值
,
从而当且仅当x=y=
时,z有最小值为
-2=
.
| 1 |
| x |
| 1 |
| y |
| 1 |
| xy |
| y |
| x |
| x |
| y |
| 1 |
| xy |
| (x+y)2-2xy |
| xy |
| 2 |
| xy |
令t=xy,则0<t=xy≤(
| x+y |
| 2 |
| 1 |
| 4 |
由f(t)=t+
| 2 |
| t |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| t |
| 33 |
| 4 |
从而当且仅当x=y=
| 1 |
| 2 |
| 33 |
| 4 |
| 25 |
| 4 |
点评:本题考查基本不等式的应用:求最值.基本不等式求最值时要注意三个原则:一正,即各项的取值为正;二定,即各项的和或积为定值;三相等,即要保证取等号的条件成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
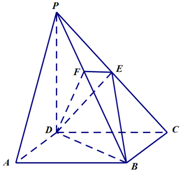 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC⊥底面ABCD,PD=DC,∠PDC=90°,E是PC的中点.