题目内容
函数y=xlnx的导数是 ．
考点：导数的运算
专题：导数的概念及应用
分析：根据导数的公式，即可得到结论．
解答：
解：∵y=xlnx
∴y′=lnx+x•
=1+lnx，
故答案为：1+lnx
∴y′=lnx+x•
| 1 |
| x |
故答案为：1+lnx
点评：本题主要考查函数的导数的计算，要求熟练掌握常见函数的导数公式，比较基础．
练习册系列答案
相关题目
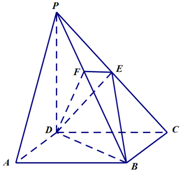如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PDC⊥底面ABCD，PD=DC，∠PDC=90°，E是PC的中点．
如图所示，对大于或等于2的自然数M的n次幂进行如下方式的“分裂”：依此类推，20143“分裂”中最大的数是若存在实数x使|x-a|+|x-1|≤3成立，则实数a的取值范围是（ ）
| A、-1＜a≤3 |
| B、-1≤a≤3 |
| C、-2≤a＜4 |
| D、-2≤a≤4 |