题目内容
20.设a=($\frac{5}{3}$)${\;}^{\frac{1}{6}}$,b=($\frac{3}{5}$)${\;}^{-\frac{1}{5}}$,c=ln$\frac{5}{3}$,则a,b,c的大小关系是( )| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:b=($\frac{3}{5}$)${\;}^{-\frac{1}{5}}$=$(\frac{5}{3})^{\frac{1}{5}}$>($\frac{5}{3}$)${\;}^{\frac{1}{6}}$=a>1,c=ln$\frac{5}{3}$<1,
∴b>a>c.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
10.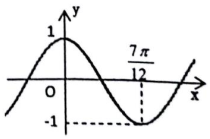 设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )
设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )
 设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )
设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )| A. | [$\frac{7kπ}{6}$-$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{7π}{24}$](k∈Z) | B. | [$\frac{7kπ}{3}$-$\frac{7π}{24}$,$\frac{7kπ}{3}$+$\frac{7π}{24}$](k∈Z) | ||
| C. | [$\frac{7kπ}{3}$-$\frac{7π}{12}$,$\frac{7kπ}{3}$+$\frac{7π}{12}$](k∈Z) | D. | [$\frac{7kπ}{6}$+$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{21π}{24}$](k∈Z) |
8.若a为实数,且(2+ai)(a-2i)=4-3i,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
12.某大学有甲、乙两个图书馆,对其借书的等待时间进行调查,得到下表:
甲图书馆
乙图书馆
(1)分别求在甲、乙两图书馆借书的平均等待时间;
(2)以表中等待时间的学生人数的频率为概率,若某同学希望借书等待时间不超过3分钟,请问在哪个图书馆借更能满足他的要求?
甲图书馆
| 借书等待时间T1(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1500 | 1000 | 500 | 500 | 1500 |
| 借书等待时间T2(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1000 | 500 | 2000 | 1250 | 250 |
(2)以表中等待时间的学生人数的频率为概率,若某同学希望借书等待时间不超过3分钟,请问在哪个图书馆借更能满足他的要求?
9.已知函数f(x)在定义域R上的导函数为f′(x),若方程f'(x)=0无解,且f[f(x)-2017x]=2017,当g(x)=sinx-cosx-kx在[-$\frac{π}{2}$,$\frac{π}{2}$]上与f(x)在R上的单调性相同时,则实数k的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,$\sqrt{2}$] | C. | [-1,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
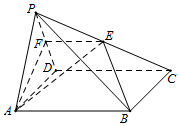 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F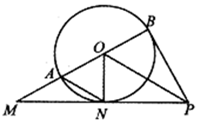 如图所示,已知AB为⊙O的直径,PB、PN都是⊙O的切线,切点分别为B、N,PN交BA的延长线于点M.
如图所示,已知AB为⊙O的直径,PB、PN都是⊙O的切线,切点分别为B、N,PN交BA的延长线于点M.