题目内容
16.若${∫}_{1}^{t}$(-$\frac{1}{x}$+2x)dx=3-ln2,则t=2.分析 利用微积分基本定理计算${∫}_{1}^{t}$(-$\frac{1}{x}$+2x)dx,列方程解出t即可.
解答 解:∵${∫}_{1}^{t}$(-$\frac{1}{x}$+2x)dx=(-lnx+x2)|$\left.\begin{array}{l}{t}\\{1}\end{array}\right.$=-lnt+t2-1,
∴3-ln2=-lnt+t2-1,解得t=2.
故答案为:2.
点评 本题考查了微积分基本定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知集合A={x||x|≤2,x∈Z},$B=\left\{{x|\frac{1}{x+1}≤0,x∈R}\right\}$,则A∩∁RB=( )
| A. | (-1,2] | B. | [-1,2] | C. | {-1,0,1,2} | D. | {0,1,2} |
8.若a为实数,且(2+ai)(a-2i)=4-3i,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.已知α为第二象限角.且sin2α=-$\frac{24}{25}$,则cosα-sinα的值为( )
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
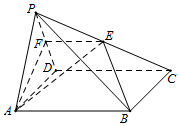 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F