题目内容
13.已知曲线M:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点是曲线N:y2=8x的焦点F,两曲线交点为P、Q,若$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则曲线M的实轴长为4$\sqrt{2}$-4.分析 求得抛物线的焦点和准线方程,可得c=2,设出P的坐标,运用抛物线的定义,可得P的坐标,代入双曲线的方程,解得a,进而得到双曲线的实轴长.
解答 解:抛物线y2=8x的焦点F(2,0),准线为x=-2,
由题意可得c=2,
$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则P,F,Q共线,设P(2,n),代入y2=8x,可得n=±4
将P(2,±4)代入双曲线的方程,可得$\frac{4}{{a}^{2}}$-$\frac{16}{{b}^{2}}$=1,且a2+b2=4,
解得a=2$\sqrt{2}$-2,
即有双曲线的实轴长为2a=4$\sqrt{2}$-4.
故答案为:4$\sqrt{2}$-4.
点评 本题考查双曲线的实轴长,注意运用抛物线的定义、方程和性质,点满足双曲线方程,考查运算能力,属于中档题.

练习册系列答案
相关题目
4.已知集合A={x||x|≤2,x∈Z},$B=\left\{{x|\frac{1}{x+1}≤0,x∈R}\right\}$,则A∩∁RB=( )
| A. | (-1,2] | B. | [-1,2] | C. | {-1,0,1,2} | D. | {0,1,2} |
8.若a为实数,且(2+ai)(a-2i)=4-3i,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
18.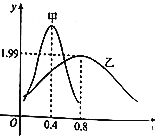 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )| A. | 乙类水果的质量服从的正态分布的参数σ2=1.99 | |
| B. | 甲类水果的质量比乙类水果的质量更集中 | |
| C. | 甲类水果的平均质量μ1=0.4kg | |
| D. | 甲类水果的平均质量比乙类水果的平均质量小 |
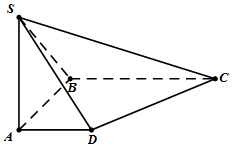 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.