题目内容
15.在△ABC中,角A,B,C的对边分别是a,b,c,其外接圆的半径是1,且满足2(sin2A-sin2C)=($\sqrt{2}$a-b)sinB.(Ⅰ)求角C的大小;
(Ⅱ)求△ABC面积的最大值.
分析 (Ⅰ)用正弦定理化简已知等式,整理后再用余弦定理变形,求出cosC的值,从而求出C的度数;
(Ⅱ)由C的度数求出A+B的度数,用A表示出B,用三角形的面积公式列出关系式,用正弦定理化简后,利用两角和与差的正弦函数公式化简,根据正弦函数的图象与性质求出最大值.
解答 解:(Ⅰ)△ABC中,其外接圆的半径是1,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R=2,
∴sinA=$\frac{a}{2}$,sinB=$\frac{b}{2}$,sinC=$\frac{c}{2}$;
又2(sin2A-sin2C)=($\sqrt{2}$a-b)sinB,
∴2($\frac{{a}^{2}}{4}$-$\frac{{c}^{2}}{4}$)=($\sqrt{2}$a-b)•$\frac{b}{2}$,
即a2+b2-c2=$\sqrt{2}$ab,
∴cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=$\frac{\sqrt{2}}{2}$;
又C∈(0,π),
∴C=$\frac{π}{4}$;
(Ⅱ))∵C=$\frac{π}{4}$,∴A+B=$\frac{3π}{4}$,即B=$\frac{3π}{4}$-A,
∵$\frac{a}{sinA}$=$\frac{b}{sinB}$=2,即a=2sinA,b=2sinB,
∴S△ABC=$\frac{1}{2}$absinC=2sinAsinBsin$\frac{π}{4}$
=$\sqrt{2}$sinAsinB
=$\sqrt{2}$sinAsin($\frac{3π}{4}$-A)
=$\sqrt{2}$sinA($\frac{\sqrt{2}}{2}$cosA+$\frac{\sqrt{2}}{2}$sinA)
=sinAcosA+sin2A
=$\frac{1}{2}$sin2A+$\frac{1}{2}$(1-cos2A)
=$\frac{\sqrt{2}}{2}$($\frac{\sqrt{2}}{2}$sin2A-$\frac{\sqrt{2}}{2}$cos2A)+$\frac{1}{2}$
=$\frac{\sqrt{2}}{2}$sin(2A-$\frac{π}{4}$)+$\frac{1}{2}$,
当2A-$\frac{π}{4}$=$\frac{π}{2}$,即A=$\frac{3π}{8}$时,△ABC的面积取得最大值为$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$.
点评 本题考查了正弦、余弦定理,三角恒等变换以及三角形的面积公式应用问题,是综合题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案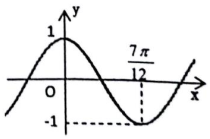 设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )
设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )| A. | [$\frac{7kπ}{6}$-$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{7π}{24}$](k∈Z) | B. | [$\frac{7kπ}{3}$-$\frac{7π}{24}$,$\frac{7kπ}{3}$+$\frac{7π}{24}$](k∈Z) | ||
| C. | [$\frac{7kπ}{3}$-$\frac{7π}{12}$,$\frac{7kπ}{3}$+$\frac{7π}{12}$](k∈Z) | D. | [$\frac{7kπ}{6}$+$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{21π}{24}$](k∈Z) |
| A. | $[-\frac{5π}{6},\frac{7π}{6}]$ | B. | $[\frac{7π}{6},\frac{19π}{6}]$ | C. | $[-\frac{2π}{3},\frac{4π}{3}]$ | D. | $[-\frac{17π}{6},-\frac{5π}{6}]$ |
| A. | (-1,2] | B. | [-1,2] | C. | {-1,0,1,2} | D. | {0,1,2} |
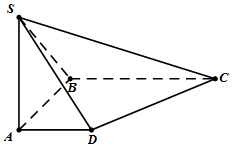 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.