题目内容
18.已知平面向量$\overrightarrow a,\overrightarrow b$满足$\overrightarrow b•(\overrightarrow a+\overrightarrow b)=3$,且$|\overrightarrow a|=1,|\overrightarrow b|=2$,则向量$\overrightarrow a$与$\overrightarrow b$的夹角( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根据平面向量的数量积公式与夹角公式,求出cosθ与θ的值.
解答 解:设向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,θ∈[0,π]
由$\overrightarrow{b}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=3可得$\overrightarrow{b}$•$\overrightarrow{a}$+${\overrightarrow{b}}^{2}$=3,
代入数据可得2×1×cosθ+22=3,
解得cosθ=-$\frac{1}{2}$,
∴θ=$\frac{2π}{3}$.
故选:C.
点评 本题考查了数量积与两个向量的夹角问题,是基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.已知α为第二象限角.且sin2α=-$\frac{24}{25}$,则cosα-sinα的值为( )
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
10.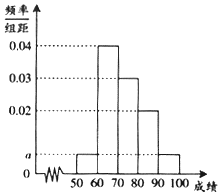 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)
 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x::y | 1:1 | 2:1 | 3:4 | 4:5 |
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)