题目内容
10.在空间直角坐标系中,已知点A(1,2,1),B(1,1,0),C(0,2,0),则以三点为顶点构成的三角形的形状是等边三角形 .分析 利用空间距离公式求出三角形三个边的边长,即可判断三角形的形状.
解答 解:因为:A(1,2,1),B(1,1,0),C(0,2,0),
所以:AB=$\sqrt{(1-1)^{2}+(2-1)^{2}+(1-0)^{2}}$=$\sqrt{2}$,
BC=$\sqrt{(1-0)^{2}+(1-2)^{2}+(0-0)^{2}}$=$\sqrt{2}$,
AC=$\sqrt{(1-0)^{2}+(2-2)^{2}+(1-0)^{2}}$=$\sqrt{2}$.
所以:AB=BC=AC,
所以:该三角形是等边三角形.
故答案是:等边三角形.
点评 本题考查三角形形状的判断,空间两点距离公式的应用,考查计算能力,属于基础题.

练习册系列答案
相关题目
20.某四棱台的三视图如图所示,则该四棱台的侧面积是( )
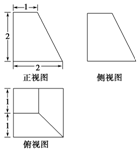

| A. | 12 | B. | $\frac{14}{3}$ | C. | $6+3\sqrt{5}$ | D. | $11+3\sqrt{5}$ |
5.函数$f(x)=\frac{{\sqrt{x+2}}}{{{2^x}-1}}$的定义域为( )
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-2,0)∪(0,+∞) | D. | [-2,0)∪(0,+∞) |
19..已知数列{an}的通项公式为an=n•($\frac{3}{4}$)n,则数列{an}的最大项是( )
| A. | a1 | B. | a3 | C. | a5 | D. | 不能确定 |
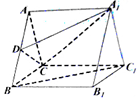 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB的中点.