题目内容
20.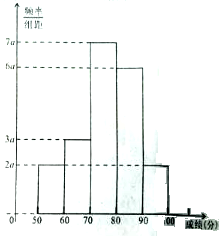 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,60)的学生中任选2人,求这两人的成绩都在[60,70)中的概率.
分析 (1)根据频率分布直方图求出a的值;
(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20乘以对应的频率,即得对应区间内的人数,从而求出所求.
(3)分别列出满足[50,70)的基本事件,再找到在[60,70)的事件个数,根据古典概率公式计算即可.
解答 解:(1)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(3)记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,
则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,
故所求概率为P=$\frac{3}{10}$.
点评 本题考查频率分布直方图的应用以及古典概型的概率的应用,属于中档题.

练习册系列答案
相关题目
10.如图是一个算法的流程图,若输入x的值为4,则输出y的值 是( )


| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
5.函数$f(x)=\frac{{\sqrt{x+2}}}{{{2^x}-1}}$的定义域为( )
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-2,0)∪(0,+∞) | D. | [-2,0)∪(0,+∞) |
12.若i是虚数单位,则复数$z=\frac{{1-\sqrt{3}i}}{2i}$在复平面内所对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
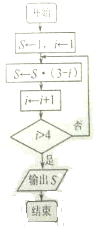 阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.
阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.