题目内容
16．向量$\overrightarrow{AB}$，$\overrightarrow{CD}$，$\overrightarrow{EF}$在正方形网格中的位置如图所示，则（ ）
| A． | $\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$ | B． | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{1}{3}$$\overrightarrow{CD}$ | C． | $\overrightarrow{EF}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$ | D． | $\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$$+\frac{2}{3}$$\overrightarrow{CD}$ |
分析 设出向量的坐标，根据坐标运算判断即可．
解答 解：设$\overrightarrow{EF}$=（0，2），则$\overrightarrow{AB}$=（1，1），$\overrightarrow{CD}$=（-1，2），
故$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{CD}$=（$\frac{2}{3}$-$\frac{2}{3}$，$\frac{2}{3}$+$\frac{4}{3}$）=（0，2），
故选：D．
点评 本题考查了向量的坐标运算，设出向量坐标是解题的关键，本题是一道基础题．
练习册系列答案
相关题目
6．函数y=x3+x+1递增区间是（ ）
| A． | （0，+∞） | B． | （-∞，1） | C． | （-∞，+∞） | D． | （1，+∞） |
7．
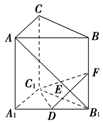直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（ ）
直三棱柱ABC-A1B1C1中，侧棱长为2，AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E，要使AB1⊥平面C1DF，则线段B1F的长为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
4．已知m，n是满足m+n=1，且使$\frac{1}{m}+\frac{9}{n}$取得最小值的正实数，若函数y=xa过点 P（m，$\frac{2}{3}$n），则α的值为（ ）
| A． | 3 | B． | 2 | C． | $\frac{1}{2}$ | D． | -1 |
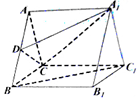如图，在直三棱柱ABC-A1B1C1中，底面△ABC是边长为2的等边三角形，D为AB的中点．
5．函数$f（x）=\frac{{\sqrt{x+2}}}{{{2^x}-1}}$的定义域为（ ）
| A． | [-2，+∞） | B． | （-2，+∞） | C． | （-2，0）∪（0，+∞） | D． | [-2，0）∪（0，+∞） |