题目内容
11．已知幂函数y=f（x）的图象经过点（$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$），则lg[f（2）]+lg[f（5）]=$\frac{1}{2}$．分析 设出幂函数的解析式，把点（$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$）代入可得解析式，再计算对应的数值即可．
解答 解：设幂函数f（x）=xα，把点（$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$）代入可得
$\frac{\sqrt{2}}{2}$=${（\frac{1}{2}）}^{α}$，
解得α=$\frac{1}{2}$；
∴f（x）=$\sqrt{x}$；
∴lg[f（2）]+lg[f（5）]=lg$\sqrt{2}$+lg$\sqrt{5}$=lg$\sqrt{10}$=$\frac{1}{2}$lg10=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查了幂函数的定义与应用问题，属于基础题．
练习册系列答案
相关题目
2．已知函数y=f（2x）+2x是偶函数，且f（2）=1，则f（-2）=（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
19．已知f（x）是定义在R上的偶函数，且f（x）在[0，+∞）是减函数，若f（lgx）＞f（1），则x的取值范围是（ ）
| A． | $（\frac{1}{10}，10）$ | B． | （0，10） | C． | （10，+∞） | D． | $（0，\frac{1}{10}）∪（10，+∞）$ |
6．一梯形的直观图是如图是欧式的等腰梯形，且直观图OA′B′C′的面积为2，则原梯形的面积为（ ）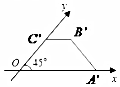
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 4 | D． | 4$\sqrt{2}$ |
16．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F，若F关于直线$\sqrt{3}$x+y=0的对称点A是椭圆C上的点，则椭圆C的离心率为（ ）
| A． | $\sqrt{2}$-1 | B． | $\sqrt{3}$-1 | C． | $\sqrt{5}$-2 | D． | $\sqrt{6}$-2 |
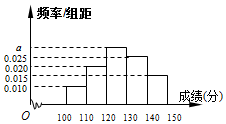某学校对高二年级期中考试数学成绩进行分析，随机抽取了分数在[100，150]的1000名学生的成绩，并根据这1000名学生的成绩画出频率分布直方图（如图所示），则成绩在[120，130）内的学生共有300人．