题目内容
1.已知f(x)是定义域为R的奇函数,若?x∈R,f′(x)>-2,则不等式f(x-1)<x2(3-2lnx)+3(1-2x)的解集是( )| A. | (0,1) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,1) |
分析 构造函数g(x),求函数的导数,判断函数的单调性,利用函数的单调性进行求解即可.
解答 解:设g(x)=f(x-1)-x2(3-2lnx)-3(1-2x),
则g′(x)=f′(x-1)+4xlnx-4x+6,
设h(x)=4xlnx-4x+6,则h′(x)=4lnx,
由h′(x)>0得x>1,
由h′(x)<0得0<x<1,
即当x=1时,函数h(x)取得极小值同时也是最小值h(1)=2,
∵f′(x-1)>-2,h(x)≥2,
∴f′(x-1)+h(x)>-2+2=0,
即g′(x)=f′(x-1)-x2(3-2lnx)-3(1-2x)>0,
即g(x)在(0,+∞)上为增函数,
则当x=1时,g(1)=f(1-1)-12(3-2ln1)-3(1-2)=0,
则不等式f(x-1)<x2(3-2lnx)+3(1-2x)等价为g(x)<0,即g(x)<g(1),
则x<1,
即不等式f(x-1)<x2(3-2lnx)+3(1-2x)的解集是(0,1),
故选:A.
点评 本题主要考查不等式的求解,构造函数,求函数的导数,利用导数和函数单调性之间的关系是解决本题的关键.综合性较强.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
6.已知弧度数为2的圆心角所对的弦长是4,则这个圆心角所对的弧长是( )
| A. | 4 | B. | $\frac{4}{sin1}$ | C. | 4sin1 | D. | sin2 |
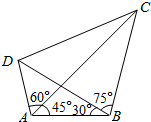 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.