题目内容
已知△ABC的顶点A是定点，边BC在定直线l上滑动，|BC|=4，BC边上的高为3，求△ABC的外心M的轨迹方程．考点：轨迹方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：建立直角坐标系，设出点的坐标，线段BC的中点，AC的中点，由
⊥
，
⊥
，可得结论．
| BC |
| PM |
| AC |
| QM |
解答：
解：建立如图所示的直角坐标系
设A（0，3），B（x0-2，0），C（x0+2，0），外心M（x，y）
则线段BC的中点P（x0，0），AC的中点Q（
，
）
∴
=（4，0），
=（x0+2，-3），
=（x-x0，y），
=（x-
，y-
），
由
⊥
，
⊥
，可得
消去x0可得：x2-6y+5=0．
解：建立如图所示的直角坐标系设A（0，3），B（x0-2，0），C（x0+2，0），外心M（x，y）
则线段BC的中点P（x0，0），AC的中点Q（
| x0+2 |
| 2 |
| 3 |
| 2 |
∴
| BC |
| AC |
| PM |
| QM |
| x0+2 |
| 2 |
| 3 |
| 2 |
由
| BC |
| PM |
| AC |
| QM |
|
消去x0可得：x2-6y+5=0．
点评：本题考查轨迹方程，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图所示的曲线C由曲线C1：
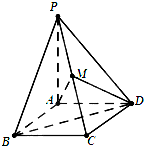在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥平面ABCD，PA=1，点M是棱PC的中点．
某次游园的一项活动中，设置了两个中奖方案：
若A、B是椭圆