题目内容
甲乙两人相约10天之内在某地会面，约定先到的人等候另一人3天后方可离开，若他们在期限内到达目的地是等可能的，则此二人会面的概率是多少？
考点：几何概型
专题：应用题,概率与统计
分析：设x表示甲到达该地点的时间，y表示乙到达该地点的时间，则0≤x≤10，0≤y≤10，整个事件空间构成一个边长为10的正方形，其中两人能会面的条件是-3≤x-y≤3，利用几何概型可求概率．
解答：
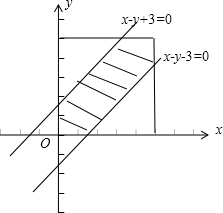解：本题考查几何概型，设x表示甲到达该地点的时间，y表示乙到达该地点的时间，则0≤x≤10，0≤y≤10
整个事件空间构成一个边长为10的正方形，其中两人能会面的条件是-3≤x-y≤3，如图，
可知两人能会面的概率为约束条件对应的可行域的面积与正方形的面积的比，
即P=
=
．
解：本题考查几何概型，设x表示甲到达该地点的时间，y表示乙到达该地点的时间，则0≤x≤10，0≤y≤10整个事件空间构成一个边长为10的正方形，其中两人能会面的条件是-3≤x-y≤3，如图，
可知两人能会面的概率为约束条件对应的可行域的面积与正方形的面积的比，
即P=
| 100-49 |
| 100 |
| 51 |
| 100 |
点评：本题主要考查几何概型，解题的关键是用面积作为测度，利用面积比求概率．
练习册系列答案
相关题目
如图，半径为30cm的
如图所示，四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD，∠ABC=45°，AB=SA=SB=2．
已知△ABC的顶点A是定点，边BC在定直线l上滑动，|BC|=4，BC边上的高为3，求△ABC的外心M的轨迹方程．
如图所示，四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别为PC、PD、BC的中点．