题目内容
 某次游园的一项活动中,设置了两个中奖方案:
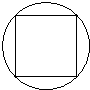
某次游园的一项活动中,设置了两个中奖方案:方案1:在如图所示的游戏盘内转动一个小球,如果小球静止时停在正方形区域内则中奖;
方案2:从一个装有2个红球和3个白球的袋中无放回地取出2个球,当两个球同色时则中奖.
两个方案中,哪个方案中奖率更高?请说明理由.
考点:几何概型
专题:概率与统计
分析:根据几何概型和古典概型的概率公式分别求出两个方案的概率,比较大小即可得到结论.
解答:
解:(1)设正方形边长为2,则圆半径为
,中奖概率为
=
=
.
(2)从袋中5个球中摸出2个,试验的结果共有4+3+2+1=10(种),
中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为1;
(ii)2个球都是白色,包含的基本事件数为2+1=3.
所以,中奖这个事件包含的基本事件数为1+3=4.
因此,中奖概率为
=
.
由于
>
,所以方案1的中奖率更高.
| 2 |
| S正方形 |
| S圆 |
| 22 | ||
π×(
|
| 2 |
| π |
(2)从袋中5个球中摸出2个,试验的结果共有4+3+2+1=10(种),
中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为1;
(ii)2个球都是白色,包含的基本事件数为2+1=3.
所以,中奖这个事件包含的基本事件数为1+3=4.
因此,中奖概率为
| 4 |
| 10 |
| 2 |
| 5 |
由于
| 2 |
| π |
| 3 |
| 5 |
点评:本题主要考查概率的计算,要求熟练掌握几何概型和古典概型的概率公式.

练习册系列答案
相关题目
 如图,三棱锥P-ABC中,∠ABC=90°,它的三视图如图所示,求该棱锥的:
如图,三棱锥P-ABC中,∠ABC=90°,它的三视图如图所示,求该棱锥的: 如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2.
如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2. 已知△ABC的顶点A是定点,边BC在定直线l上滑动,|BC|=4,BC边上的高为3,求△ABC的外心M的轨迹方程.
已知△ABC的顶点A是定点,边BC在定直线l上滑动,|BC|=4,BC边上的高为3,求△ABC的外心M的轨迹方程. 一个棱锥的三视图如图1所示,正视图和侧视图都是腰长为1的等腰直角三角形,俯视图是边长为1的正方形.
一个棱锥的三视图如图1所示,正视图和侧视图都是腰长为1的等腰直角三角形,俯视图是边长为1的正方形.