题目内容
函数f（x）=
的定义域为A，函数g（x）=
的定义域为B，若A∩B=∅，求实数a的取值范围．
|
| 2-|x+a| |
考点：函数的定义域及其求法
专题：计算题,函数的性质及应用
分析：由题意可得A=（-∞，-1）∪（4，+∞）；B⊆[-1，4]；由2-|x+a|≥0得-2-a≤x≤2-a，从而解得．
解答：
解：由题意，x2-3x-4＞0；
故A=（-∞，-1）∪（4，+∞）；
∵A∩B=∅，
∴B⊆[-1，4]；
由2-|x+a|≥0得，
|x+a|≤2；
故-2-a≤x≤2-a；
故-1≤-2-a≤2-a≤4，
解得，-2≤a≤-1．
故A=（-∞，-1）∪（4，+∞）；
∵A∩B=∅，
∴B⊆[-1，4]；
由2-|x+a|≥0得，
|x+a|≤2；
故-2-a≤x≤2-a；
故-1≤-2-a≤2-a≤4，
解得，-2≤a≤-1．
点评：本题考查了函数的定义域的求法，属于基础题．
练习册系列答案
相关题目
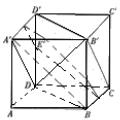如图，ABCD-A1B1C1D1为正方体，任作平面a与对角线AC′垂直，使得a与正方体的每个面都有公共点，记这样得到的截面多边形的面积为S，周长为l，则（ ）| A、S为定值，l不为定值 |
| B、S不为定值，l为定值 |
| C、S与l均为定值 |
| D、S与l均不为定值 |
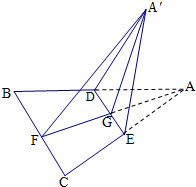已知边长为a的正△ABC的中线AF与中位线DE相交于点G，现将△AED沿DE翻折为△A′ED，如图是翻折过程中的一个图形，则下列四个结论：