题目内容
函数y=sinx-cosx+sinxcosx,x∈[0,π]的最大值是 ,最小值是 .
考点:三角函数的最值
专题:三角函数的求值
分析:设sinx-cosx=t,得sinxcosx的函数关系式,依题意结合x的范围,求出t的范围,利用二次函数闭区间上的最值求解即可.
解答:
解:设sinx-cosx=t,则(sinx-cosx)2=t2⇒sinxcosx=
,
∵x∈[0,π],
∴(x-
)∈[-
,
],sin(x-
)∈[-
,1],
∴t=sinx-cosx=
sin(x-
)∈[-1,
],
∴y=-
t2+t+
=-
(t-1)2+1,
∴当t=1时,ymax=1;
当t=-1时,ymin=-1.
∴函数y=sinx-cosx+sinxcosx,x∈[0,π]的值域是[-1,1].
函数的最大值为1,最小值为-1.
故答案为:1;-1.
| 1-t2 |
| 2 |
∵x∈[0,π],
∴(x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴t=sinx-cosx=
| 2 |
| π |
| 4 |
| 2 |
∴y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当t=1时,ymax=1;
当t=-1时,ymin=-1.
∴函数y=sinx-cosx+sinxcosx,x∈[0,π]的值域是[-1,1].
函数的最大值为1,最小值为-1.
故答案为:1;-1.
点评:本题考查三角函数的最值,换元是关键,考查等价转化思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
下列四个命题( )
①函数y=x2-5x+4在x∈[-1,1]上的最大值为10,最小值为
;
②函数y=2x2-4x+1(2<x<4)的最大值为17,最小值为1;
③函数y=x3-12x(-3<x<4)的最大值为16,最小值为-16;
④函数y=x3-12x(-2<x<2)无最大值也无最小值.
①函数y=x2-5x+4在x∈[-1,1]上的最大值为10,最小值为
| 9 |
| 4 |
②函数y=2x2-4x+1(2<x<4)的最大值为17,最小值为1;
③函数y=x3-12x(-3<x<4)的最大值为16,最小值为-16;
④函数y=x3-12x(-2<x<2)无最大值也无最小值.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知函数f(x)在R上满足f(1+x)=2f(1-x)-x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、3x-y-2=0 |
| B、3x+y-2=0 |
| C、x-y+1=0 |
| D、x-y-2=0 |
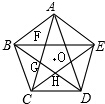 如图,求边长为1的正五边形的对角线围成的正五边形的边长.
如图,求边长为1的正五边形的对角线围成的正五边形的边长.