题目内容
已知椭圆C：
+
=1（a＞b＞0）的左，右焦点分贝为F1，F2，右顶点为A，P为椭圆C上一点，
•
的最大值为3，最小值为2．
（1）求椭圆C的方程．
（2）若直线l过点（
，0），且与椭圆C交于M、N两点．
①若直线l与x轴垂直，证明MA⊥NA．
②求证：以MN为直径的圆过一定点，并求出该点坐标．
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
（1）求椭圆C的方程．
（2）若直线l过点（
| 2 |
| 7 |
①若直线l与x轴垂直，证明MA⊥NA．
②求证：以MN为直径的圆过一定点，并求出该点坐标．
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：（1）设出椭圆上点P的参数坐标，代入
•
，求出
•
的最大值a2-c2=3，最小值b2-c2=2，结合隐含条件求得a2=4，b2=3，则椭圆方程可求；
（2）①写出过定点（
，0）且与x轴垂直的直线l的方程为x=
，代入椭圆方程求得M，N的坐标，进一步求出
，
的坐标，由数量积为0得答案；
②设直线l：y=kx+m，M（x1，y1），N（x2，y2），求出以MN为直径的圆方程（x-x1）（x-x2）+（y-y1）（y-y2）=0，结合A（2，0）在圆上得到（2-x1）（2-x2）+y1y2=0，再由于M，N在直线l上化纵坐标为横坐标，联立
直线方程和椭圆方程，利用根与系数关系解得m=-2k 或 m=-
．验证m=-2k时不合题意，求得当m=-
时直线l过定点（
，0）．
| PF1 |
| PF2 |
| PF1 |
| PF2 |
（2）①写出过定点（
| 2 |
| 7 |
| 2 |
| 7 |
| MA |
| NA |
②设直线l：y=kx+m，M（x1，y1），N（x2，y2），求出以MN为直径的圆方程（x-x1）（x-x2）+（y-y1）（y-y2）=0，结合A（2，0）在圆上得到（2-x1）（2-x2）+y1y2=0，再由于M，N在直线l上化纵坐标为横坐标，联立
直线方程和椭圆方程，利用根与系数关系解得m=-2k 或 m=-
| 2k |
| 7 |
| 2k |
| 7 |
| 2 |
| 7 |
解答：
解：（1）利用椭圆的参数方程，
设P（acosθ，bsinθ），F1（-c，0），F2（c，0），
则：
•
=（-c-acosθ，-bsinθ）•（c-acosθ，-bsinθ）
=（acosθ+c）（acosθ-c）+（bsinθ）2
=a2cos2θ-c2+b2（1-cos2θ）
=（a2-b2）cos2θ+（b2-c2）．
则当cos2θ=1时，
•
取最大值a2-c2=3，
当cos2θ=0时，
•
取最小值b2-c2=2，
又a2=b2+c2，
联立以上几式解得：a2=4，b2=3．
则椭圆C：
+
=1；
（2）①证明：直线l过定点（
，0），且与x轴垂直，
则l的方程为x=
，代入椭圆方程得：M（
，
），N（
，-
），
又A（2，0），
∴
=(
，-
)，
=(
，
)，
则
•
=
×
-
×
=0，
∴MA⊥NA；
②设直线l：y=kx+m，
M（x1，y1），N（x2，y2），
则以MN为直径的圆方程：
（x-x1）（x-x2）+（y-y1）（y-y2）=0，
由于C的右顶点A（2，0）在圆上，
则：（2-x1）（2-x2）+y1y2=0，
x1x2+4-2（x1+x2）+y1y2=0 （*）．
由于M，N在直线l上，
则：y1=kx1+m，y2=kx2+m，
代入（*）得：
(1+k2)x1x2+(mk-2)(x1+x2)+m2+4=0 （#）．
联立
，得（3+4k2）x2+8kmx+4m2-12=0．
则：x1+x2=-
，x1x2=
，
代入（#）得：(1+k2)•
+(mk-2)•(-
)+m2+4=0．
整理得：4k2+16km+7m2=0．
即（2k+m）（2k+7m）=0．
解得：m=-2k 或 m=-
．
又∵m=-2k时，l：y=kx+m=k（x-2）恒过C的右顶点A（2，0），
故m=-2k（舍去），
则m=-
．
l：y=kx-
=k（x-
），
即直线l过定点（
，0）．
设P（acosθ，bsinθ），F1（-c，0），F2（c，0），
则：
| PF1 |
| PF2 |
=（acosθ+c）（acosθ-c）+（bsinθ）2
=a2cos2θ-c2+b2（1-cos2θ）
=（a2-b2）cos2θ+（b2-c2）．
则当cos2θ=1时，
| PF1 |
| PF2 |
当cos2θ=0时，
| PF1 |
| PF2 |
又a2=b2+c2，
联立以上几式解得：a2=4，b2=3．
则椭圆C：
| x2 |
| 4 |
| y2 |
| 3 |
（2）①证明：直线l过定点（
| 2 |
| 7 |
则l的方程为x=
| 2 |
| 7 |
| 2 |
| 7 |
| 12 |
| 7 |
| 2 |
| 7 |
| 12 |
| 7 |
又A（2，0），
∴
| MA |
| 12 |
| 7 |
| 12 |
| 7 |
| NA |
| 12 |
| 7 |
| 12 |
| 7 |
则
| MA |
| NA |
| 12 |
| 7 |
| 12 |
| 7 |
| 12 |
| 7 |
| 12 |
| 7 |
∴MA⊥NA；
②设直线l：y=kx+m，
M（x1，y1），N（x2，y2），
则以MN为直径的圆方程：
（x-x1）（x-x2）+（y-y1）（y-y2）=0，
由于C的右顶点A（2，0）在圆上，
则：（2-x1）（2-x2）+y1y2=0，
x1x2+4-2（x1+x2）+y1y2=0 （*）．
由于M，N在直线l上，
则：y1=kx1+m，y2=kx2+m，
代入（*）得：
(1+k2)x1x2+(mk-2)(x1+x2)+m2+4=0 （#）．
联立
|
则：x1+x2=-
| 8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
代入（#）得：(1+k2)•
| 4m2-12 |
| 3+4k2 |
| 8km |
| 3+4k2 |
整理得：4k2+16km+7m2=0．
即（2k+m）（2k+7m）=0．
解得：m=-2k 或 m=-
| 2k |
| 7 |
又∵m=-2k时，l：y=kx+m=k（x-2）恒过C的右顶点A（2，0），
故m=-2k（舍去），
则m=-
| 2k |
| 7 |
l：y=kx-
| 2k |
| 7 |
| 2 |
| 7 |
即直线l过定点（
| 2 |
| 7 |
点评：本题考查了椭圆方程的求法，训练了椭圆的参数方程的应用，考查了直线与圆锥曲线的位置关系，涉及直线与圆锥曲线关系问题，常采用联立直线与圆锥曲线，化为关于x的一元二次方程，然后利用根与系数关系求解，考查了计算能力，是压轴题．
练习册系列答案
相关题目
椭圆C：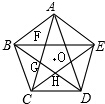
如图，求边长为1的正五边形的对角线围成的正五边形的边长．