题目内容
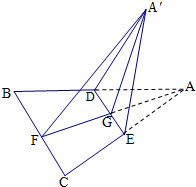 已知边长为a的正△ABC的中线AF与中位线DE相交于点G,现将△AED沿DE翻折为△A′ED,如图是翻折过程中的一个图形,则下列四个结论:
已知边长为a的正△ABC的中线AF与中位线DE相交于点G,现将△AED沿DE翻折为△A′ED,如图是翻折过程中的一个图形,则下列四个结论:①动直线A′F与直线DE互相垂直;
②恒有平面A′GF⊥平面BCED;
③四棱锥A′-BCED的体积有最大值;
④三棱锥A′-DEF的侧面积没有最大值.
其中正确结论的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:平面与平面垂直的性质,棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:由线面垂直的判定定理、性质定理由三棱锥的体积公式等进行判断.
解答:
解:因为已知边长为a的正△ABC的中线AF与中位线DE相交于点G,所以DE⊥AG,DE⊥A′G,所以DE⊥平面A′FG,
所以DE⊥A′F;故①正确;
②由①得DE?平面BCED,所以平面A′GF⊥平面BCED;故②正确;
③三棱锥A′-FED的底面积是定值,体积由高即A′到底面的距离决定,当平面A′DE⊥平面BCED时,三棱锥A′-FED的体积有最大值,故③正确;
故选C.
所以DE⊥A′F;故①正确;
②由①得DE?平面BCED,所以平面A′GF⊥平面BCED;故②正确;
③三棱锥A′-FED的底面积是定值,体积由高即A′到底面的距离决定,当平面A′DE⊥平面BCED时,三棱锥A′-FED的体积有最大值,故③正确;
故选C.
点评:本题考查了线面、面面垂直的判定定理、性质定理的运用,考查了空间线线、线面的位置关系及三棱锥体积的计算,考查了空间想象能力.

练习册系列答案
相关题目
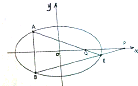
已知点F1、F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,过点F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2是直角三角形,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、1+
| ||
D、2+
|
已知函数f(x)在R上满足f(1+x)=2f(1-x)-x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、3x-y-2=0 |
| B、3x+y-2=0 |
| C、x-y+1=0 |
| D、x-y-2=0 |
 椭圆C:
椭圆C: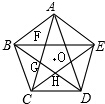 如图,求边长为1的正五边形的对角线围成的正五边形的边长.
如图,求边长为1的正五边形的对角线围成的正五边形的边长.