题目内容
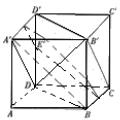如图，ABCD-A1B1C1D1为正方体，任作平面a与对角线AC′垂直，使得a与正方体的每个面都有公共点，记这样得到的截面多边形的面积为S，周长为l，则（ ）| A、S为定值，l不为定值 |
| B、S不为定值，l为定值 |
| C、S与l均为定值 |
| D、S与l均不为定值 |
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：将正方体切去两个正三棱锥A-A′BD与C′-D′B′C后，得到一个以平行平面A′BD与D′B′C为上、下底面的几何体V，V的每个侧面都是等腰直角三角形，截面多边形W的每一条边分别与V的底面上的一条边平行，将V的侧面沿棱A′B′剪开，展平在一张平面上，得到一个?A′B′B1A1，考查E′的位置，确定S，l．
解答：
解：将正方体切去两个正三棱锥A-A′BD与C′-D′B′C后，得到一个以平行平面A′BD与D′B′C为上、下底面的几何体V，V的每个侧面都是等腰直角三角形，截面多边形W的每一条边分别与V的底面上的一条边平行，将V的侧面沿棱A′B′剪开，展平在一张平面上，得到一个?A′B′B1A1，如图
而多边形W的周界展开后便成为一条与A′A1平行的线段（如图中E′E1），显然E′E1=A′A1，故l为定值．
当E′位于A′B′中点时，多边形W为正六边形，而当E′移至A′处时，W为正三角形，易知周长为定值l的正六边形与正三角形面积分别为
l2与
l2，故S不为定值．
故选B．
而多边形W的周界展开后便成为一条与A′A1平行的线段（如图中E′E1），显然E′E1=A′A1，故l为定值．
当E′位于A′B′中点时，多边形W为正六边形，而当E′移至A′处时，W为正三角形，易知周长为定值l的正六边形与正三角形面积分别为
| ||
| 24 |
| ||
| 36 |
故选B．
点评：本题考查了利用平面几何的知识解决立体几何，考查学生的空间想象能力，属于难题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目