题目内容
设数列{an}满足:a1=1,an+1=2an+1(n∈N*)
(Ⅰ)证明数列{an+1}为等比数列,并求出数列{an}的通项公式;
(Ⅱ)若bn=log2(an+1),求数列{
}的前n项和Sn.
(Ⅰ)证明数列{an+1}为等比数列,并求出数列{an}的通项公式;
(Ⅱ)若bn=log2(an+1),求数列{
| 1 |
| bnbn+1 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知得an+1+1=2(an+1),a1+1=2,由此能证明数列{an+1}是以2为首项,以2为公比的等比数列,从而能求出an=2n-1.
(Ⅱ)由bn=log2(an+1)=n,得
=
=
-
,由此利用裂项求和法能求出数列{
}的前n项和Sn.
(Ⅱ)由bn=log2(an+1)=n,得
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| bnbn+1 |
解答:
(Ⅰ)证明:∵数列{an}满足:a1=1,an+1=2an+1(n∈N*),
∴an+1+1=2(an+1),a1+1=2,
∴数列{an+1}是以2为首项,以2为公比的等比数列,
∴an+1=2n,
∴an=2n-1.
(Ⅱ)解:∵bn=log2(an+1)=n,
∴
=
=
-
,
∴Tn=1-
+
-
+…+
-
=1-
=
.
∴an+1+1=2(an+1),a1+1=2,
∴数列{an+1}是以2为首项,以2为公比的等比数列,
∴an+1=2n,
∴an=2n-1.
(Ⅱ)解:∵bn=log2(an+1)=n,
∴
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查等比数列的证明,考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要注意裂项求和法的合理运用.

练习册系列答案
相关题目
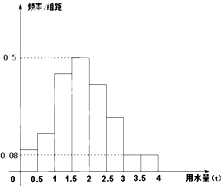 为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).