题目内容
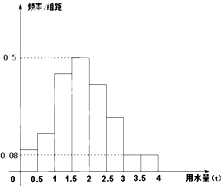 为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).(1)分别求出频率分布表中a、b的值;
(2)设A1、A2、A3是户月均用水量为[0,2)的居民代表,B1、B2是户月均用水量为[2,4]的居民代表.现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表B1、B2至少有一人被选中的概率.
| 分组 | 频数 | 频率 |
| [0,0.5) | 5 | 0.05 |
| [0.5,1) | 8 | 0.08 |
| [1,1.5) | 22 | 0.22 |
| [1.5,2) | a | |
| [2,2.5) | 20 | 0.20 |
| [2.5,3) | 12 | 0.12 |
| [3,3.5) | b | |
| [3.5,4] |
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(1)根据频率直方图的高为频率与组距的比,计算出a;根据频率=
求得b;
(2)根据古典概型的计算公式,先求五代表中任选2人的所有情况(事件),再求B1、B2至少有一人被选中的情况(事件),代入公式计算即可.
| 频数 |
| 样本数 |
(2)根据古典概型的计算公式,先求五代表中任选2人的所有情况(事件),再求B1、B2至少有一人被选中的情况(事件),代入公式计算即可.
解答:
解:(1)由频率分布直方图可得a=0.5×0.5=0.25,
∴月用水量为[1.5,2)的频数为25.
故2b=100-92=8,得b=4.
(2)由A1、A2、A3、B1、B2五代表中任选2人共有如下10种不同选法,分别为:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
记“B1、B2至少有一人被选中”的事件为A,事件A包含的基本事件为:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),
共包含7个基本事件数.
又基本事件的总数为10,所以P(A)=
.
即居民代表B1、B2至少有一人被选中的概率为P=
.
∴月用水量为[1.5,2)的频数为25.
故2b=100-92=8,得b=4.
(2)由A1、A2、A3、B1、B2五代表中任选2人共有如下10种不同选法,分别为:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
记“B1、B2至少有一人被选中”的事件为A,事件A包含的基本事件为:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),
共包含7个基本事件数.
又基本事件的总数为10,所以P(A)=
| 7 |
| 10 |
即居民代表B1、B2至少有一人被选中的概率为P=
| 7 |
| 10 |
点评:本题考查频率分布直方图及古典概型的概率计算.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目