题目内容
 如图,在△ABC中,AB=AC,过点A的直线与△ABC的外接圆交于点P,交BC的延长线于点D,
如图,在△ABC中,AB=AC,过点A的直线与△ABC的外接圆交于点P,交BC的延长线于点D,(Ⅰ)求证:∠ABP=∠D;
(Ⅱ)若AC=3,AP=2,求点D到△ABC的外接圆的切线长.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(Ⅰ)证明△ABD∽△APB,可得∠ABP=∠D;
(Ⅱ)利用∴△ABD∽△APB,可得AD=
,从而可求DP,利用切割线定理即可求出点D到△ABC的外接圆的切线长.
(Ⅱ)利用∴△ABD∽△APB,可得AD=
| 9 |
| 2 |
解答:
(Ⅰ)证明:∵AB=AC
∴∠ABC=∠ACB
又∠ACB=∠APB
∴∠ABC=∠APB
∵∠BAD=∠PAB,
∴△ABD∽△APB,
∴∠ABP=∠D;
(Ⅱ)解:∵△ABD∽△APB,
∴
=
,
∴AB=AC=3,AP=2,
∴AD=
,
∴DP=AD-AP=
,
设DE与圆相切于点E,则DE2=DP•DA=
,
∴DE=
.
∴∠ABC=∠ACB
又∠ACB=∠APB
∴∠ABC=∠APB
∵∠BAD=∠PAB,
∴△ABD∽△APB,
∴∠ABP=∠D;
(Ⅱ)解:∵△ABD∽△APB,
∴
| AB |
| AD |
| AP |
| AB |
∴AB=AC=3,AP=2,
∴AD=
| 9 |
| 2 |
∴DP=AD-AP=
| 5 |
| 2 |
设DE与圆相切于点E,则DE2=DP•DA=
| 45 |
| 4 |
∴DE=
3
| ||
| 2 |
点评:此题主要考查的是切割线定理、考查相似三角形的性质、相似三角形的判定,正确的判断出相似三角形的对应边和对应角是解答此题的关键.

练习册系列答案
相关题目
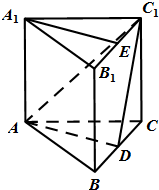 如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.
如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点. 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD= 如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PAB⊥平面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PAB⊥平面ABCD, 如图,F1,F2分别是椭圆C:
如图,F1,F2分别是椭圆C: