题目内容
 如图,F1,F2分别是椭圆C:
如图,F1,F2分别是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的离心率;
(Ⅱ)已知△AF1F2的面积为25
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)直接利用∠F1AF2=60°,求椭圆C的离心率;
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,利用余弦定理以及已知△AF1B的面积为25
,直接求a,b 的值.由此能求出|AB|.
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,利用余弦定理以及已知△AF1B的面积为25
| 3 |
解答:
解:(Ⅰ)∵F1,F2分别是椭圆C:
+
=1(a>b>0)的左、右焦点,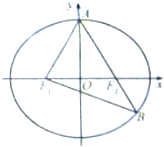
A是椭圆C的顶点,∠F1AF2=60°,
∴a=2c,
∴e=
=
.
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,
在三角形BF1F2中,|BF1|2=|BF2|2+|F1F2|2-2|BF2||F1F2|cos120°
整理,得(2a-m)2=m2+a2+am.
m=
a.
△AF1B面积S=
|BA||F1A|sin60°,
∴
a(a+
a)•
=25
,解得a=
.
∴c=
=
,∴F1(-
,0),F2(
,0),∴A(0,
),
∴直线AB:x+y-
=0
∴F1到直线AB的距离d=
=
,
∴|AB|=
=
=4
.
| x2 |
| a2 |
| y2 |
| b2 |

A是椭圆C的顶点,∠F1AF2=60°,
∴a=2c,
∴e=
| c |
| a |
| 1 |
| 2 |
(Ⅱ)设|BF2|=m,则|BF1|=2a-m,
在三角形BF1F2中,|BF1|2=|BF2|2+|F1F2|2-2|BF2||F1F2|cos120°
整理,得(2a-m)2=m2+a2+am.
m=
| 3 |
| 5 |
△AF1B面积S=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
| 3 |
5
| ||
| 2 |
∴c=
| a |
| 2 |
5
| ||
| 4 |
5
| ||
| 4 |
5
| ||
| 4 |
5
| ||
| 4 |
∴直线AB:x+y-
5
| ||
| 4 |
∴F1到直线AB的距离d=
|-
| ||||||||
|
5
| ||
| 2 |
∴|AB|=
25
| ||
|
25
| ||||
|
| 15 |
点评:本题考查椭圆离心率的求法,考查弦长的求法,解题时要认真审题,注意弦长公式和椭圆性质的灵活运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
用数学归纳法证明
+
+…+
≥
,从n=k到n=k+l,不等式左边需添加的项是( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 5 |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
过椭圆
+y2=1(a>1)的右焦点F作相互垂直的两条弦AB和CD,若|AB|+|CD|的最小值为2
,则椭圆的离心率e=( )
| x2 |
| a2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,AB=AC,过点A的直线与△ABC的外接圆交于点P,交BC的延长线于点D,
如图,在△ABC中,AB=AC,过点A的直线与△ABC的外接圆交于点P,交BC的延长线于点D,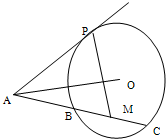 (几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为
(几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为