题目内容
6.设函数$f(x)=\left\{{\begin{array}{l}{{2^x},x<0}\\{2x-1,x≥0}\end{array}}\right.$,则f(f(-1))=0.分析 根据分段函数的表达式代入进行求解即可.
解答 解:由分段函数得f(-1)=$\frac{1}{2}$,则f($\frac{1}{2}$)=2×$\frac{1}{2}$-1=1-1=0,
故$f(f(-1))=f(\frac{1}{2})=0$.
故答案为:0
点评 本题主要考查函数值的计算,根据分段函数的表达式利用代入法是解决本题的关键.

练习册系列答案
相关题目
17.在等差数列{an}中,a3-a2=-2,a7=-2,则a9=( )
| A. | 2 | B. | -2 | C. | -4 | D. | -6 |
14.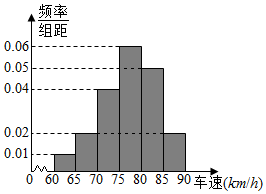 对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
 对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )| A. | 75,0.25 | B. | 80,0.35 | C. | 77.5,0.25 | D. | 77.5,0.35 |
1.下列函数在其定义域上既是奇函数又是增函数的是( )
| A. | y=x3 | B. | $y=-\frac{1}{x}$ | C. | y=tanx | D. | $y=\left\{\begin{array}{l}x(x≥0)\\-x(x<0).\end{array}\right.$ |
11.已知集合A={x|x≥4},B={x|-1≤2x-1≤0},则∁RA∩B=( )
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4) | D. | (1,4] |
18.已知31=3,32=9,33=27…,则32016的个位数上数字为( )
| A. | 1 | B. | 3 | C. | 7 | D. | 9 |