题目内容

1．下列函数在其定义域上既是奇函数又是增函数的是（　　）
A．y=x3B．$y=-\frac{1}{x}$C．y=tanxD．$y=\left\{\begin{array}{l}x（x≥0）\\-x（x＜0）.\end{array}\right.$

分析 根据函数奇偶性和单调性的性质分别进行判断即可．

解答 解：A．y=x3是奇函数在其定义域上是增函数，满足条件，
B．y=-$\frac{1}{x}$是奇函数在每个区间上为是增函数，但其定义域不是增函数，不满足条件．
C．y=tanx为奇函数，在每个区间上为是增函数，但其定义域不是增函数，不满足条件，
D．y=$\left\{\begin{array}{l}{x，x≥0}\\{-x，x＜0}\end{array}\right.$为偶函数，在定义域上不是增函数．
故选：A

点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．

练习册系列答案
相关题目
13．化简$\frac{sin（π+α）}{cos（π-α）tan（2π-α）}$=-1．
12．已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=ex（x+1），给出以下命题：
①当x＞0时，f（x）=ex（1-x）；
②f（x）有3个零点；
③f（x）＞0的解集为（-1，0）∪（1，+∞）；
④?x1，x2∈R，都有|f（x1）-f（x2）|≤2，
其中正确命题的序号是②③④（填上所有正确命题的序号）
9．已知集合$A=\{x|y=\sqrt{2-x}\}$，B={x|x2-2x＜0}，则A∩B=（　　）
A．（0，2]B．（0，2）C．（-∞，2]D．（2，+∞）
16．有三对师徒共6个人，站成一排照相，每对师徒相邻的站法共有（　　）
A．72B．54C．48D．8
6．设函数$f（x）=\left\{{\begin{array}{l}{{2^x}，x＜0}\\{2x-1，x≥0}\end{array}}\right.$，则f（f（-1））=0．
13．一几何体的三视图是如图所示的三个直角边为2的等腰直角三角形，则该几何体的表面积为（　　）
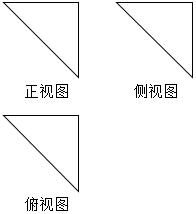
A．8B．4$\sqrt{3}$+4C．4$\sqrt{2}$+4D．6+2$\sqrt{3}$
10．已知数列{an}为等差数列，若a1，a2，a3成等比数列，且a1=1，则公差d=（　　）
A．0B．1C．2D．4
11．判断函数的奇偶性：函数f（x）=x3•1g$\frac{1-x}{1+x}$是偶函数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网