Question

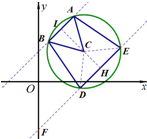已知直线l：y=x+2被圆C：（x-3）²+（y-2）²=r²（r＞0）截得的弦AB的长等于该圆的半径．
（1）求圆C的方程；
（2）已知直线m：y=x+n被圆C：（x-3）²+（y-2）²=r²（r＞0）截得的弦与圆心构成三角形CDE．若△CDE的面积有最大值，求出直线m：y=x+n的方程；若△CDE的面积没有最大值，说明理由．

Answer 1

考点：直线和圆的方程的应用

专题：直线与圆

分析：（1）根据直线和圆相交得到的弦长公式求出圆的半径即可求圆C的方程；
（2）根据直线和圆相交的位置关系，结合△CDE的面积公式即可得到结论．

解答： 解：（1）设直线l与圆C交于A，B两点．
∵直线l：y=x+2被圆C：（x-3）²+（y-2）²=r²（r＞0）截得的弦长等于该圆的半径，
∴△CAB为正三角形，
∴三角形的高等于边长的

3

2

，
∴圆心C到直线l的距离等于边长的

3

2

．
∵直线方程为x-y+2=0，圆心的坐标为（3，2），
∴圆心到直线的距离d=

|3-2+2|

1+1

=

3 2

2

=

3

2

r，
∴r=

6

，∴圆C的方程为：（x-3）²+（y-2）²=6．
（2）设圆心C到直线m的距离为h，H为DE的中点，连结CD，CH，CE．
在△CDE中，
∵DE=2

CE2-CH2

=2

6-h2

，
∴S△CDE=

1

2

DE•CH=

1

2

×2

6-h2

•h=h•

6-h2

∴S△CDE=

h2(6-h2)

≤

h2+6-h2

2

=3，
当且仅当h²=6-h²，即h²=3，解得h=

3

时，△CDE的面积最大．
∵CH=

|3-2+n|

1+1

=

2

2

•|n+1|=h=

3

，
∴|n+1|=

6

，
∴n=±

6

-1，∴存在n的值，使得△CDE的面积最大值为3，
此时直线m的方程为y=x．

点评：本题主要考查直线和圆的位置关系的应用，根据弦长公式是解决本题的关键．