题目内容
椭圆
+
=1的长轴端点A、B与y轴平行的直线交椭圆于P、Q,PA、QB延长线相交于S,求S轨迹.
| x2 |
| 16 |
| y2 |
| 8 |
考点:圆锥曲线的轨迹问题
专题:圆锥曲线的定义、性质与方程
分析:设S(x,y),P(m,n),Q(m,-n),由kPA=kAS,得
=
,由kBQ=kQS,得
=
.
两式相乘得
=
.再由P,Q两点在椭圆上得到
+
=1,结合
=
可得S的轨迹方程.
| n |
| m+a |
| y |
| x+a |
| n |
| a-m |
| y |
| x-a |
两式相乘得
| n2 |
| a2-m2 |
| y2 |
| x2-a2 |
| m2 |
| a2 |
| n2 |
| b2 |
| n2 |
| a2-m2 |
| y2 |
| x2-a2 |
解答:
解:设S(x,y),P(m,n),Q(m,-n),
kPA=
=
,kAS=
=
,
由kPA=kAS,得
=
①.
kBQ=
=
,kQS=
=
,
由kBQ=kQS,得
=
②.
由①×②得,
=
③.
又P,Q两点在椭圆上,满足
+
=1,
即
=1-
=
,则
=
=
•
,
代入③式得:
=
•
.
即
=
=
-1,
故
-
=1.
即
-
=1.
∴S的轨迹为
-
=1.
kPA=
| n-0 |
| m-(-a) |
| n |
| m+a |
| 0-y |
| -a-x |
| y |
| x+a |
由kPA=kAS,得
| n |
| m+a |
| y |
| x+a |
kBQ=
| -n-0 |
| m-a |
| n |
| a-m |
| y-0 |
| x-a |
| y |
| x-a |
由kBQ=kQS,得
| n |
| a-m |
| y |
| x-a |
由①×②得,
| n2 |
| a2-m2 |
| y2 |
| x2-a2 |
又P,Q两点在椭圆上,满足
| m2 |
| a2 |
| n2 |
| b2 |
即
| n2 |
| b2 |
| m2 |
| a2 |
| a2-m2 |
| a2 |
| b2 |
| n2 |
| a2 |
| a2-m2 |
| a2 |
| n2 |
| n2 |
| a2-m2 |
代入③式得:
| b2 |
| n2 |
| a2 |
| n2 |
| y2 |
| x2-a2 |
即
| y2 |
| b2 |
| x2-a2 |
| a2 |
| x2 |
| a2 |
故
| x2 |
| a2 |
| y2 |
| b2 |
即
| x2 |
| 16 |
| y2 |
| 8 |
∴S的轨迹为
| x2 |
| 16 |
| y2 |
| 8 |
点评:本题考查了轨迹方程的求法,考查了代入法求曲线的方程,体现了整体运算思想方法,是中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
i是虚数单位,满足
=i的复数z=( )
| z+i |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知双曲线与抛物线y2=8x有公共的焦点,且双曲线的离心率为2,则该双曲线的标准方程为( )
A、x2-
| ||
B、y2-
| ||
C、x2-
| ||
D、y2-
|
定义域是R上的函数f(x)满足f(x+2)=2f(x),当x∈(0,2]时,f(x)=
,若x∈(-4,-2]时,f(x)≤
-
有解,则实数t的取值范围是( )
|
| t |
| 4 |
| 1 |
| 2t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
 如图所示的是某一容器的三视图,现向容器中匀速注水,则容器中水面的高度h随时间t变化的图象可能是( )
如图所示的是某一容器的三视图,现向容器中匀速注水,则容器中水面的高度h随时间t变化的图象可能是( )



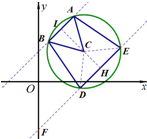 已知直线l:y=x+2被圆C:(x-3)2+(y-2)2=r2(r>0)截得的弦AB的长等于该圆的半径.
已知直线l:y=x+2被圆C:(x-3)2+(y-2)2=r2(r>0)截得的弦AB的长等于该圆的半径.