题目内容
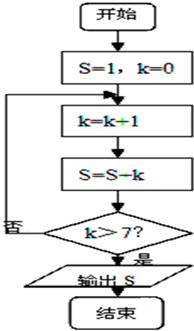执行如图所示的程序框图，则输出的结果是（ ）| A、28 | B、29 | C、36 | D、37 |
考点：程序框图
专题：算法和程序框图
分析：根据程序框图，依次计算运行的结果，直到不满足条件k＞7，即可得到S的值．
解答：
解：第一次运行k=1，S=1+1=2，不满足条件k＞7，
第二次运行k=2，S=2+2=4，不满足条件k＞7，
第三次运行k=3，S=4+3=7，不满足条件k＞7，
第四次运行k=4，S=7+4=11，不满足条件k＞7，
第五次运行k=5，S=11+5=16，不满足条件k＞7，
第六次运行k=6，S=16+6=22，不满足条件k＞7，
第七次运行k=7，S=22+7=29，不满足条件k＞7，
第八次运行k=8，S=29+8=37，此时满足条件k＞7，
输出S=37，
故选：D
第二次运行k=2，S=2+2=4，不满足条件k＞7，
第三次运行k=3，S=4+3=7，不满足条件k＞7，
第四次运行k=4，S=7+4=11，不满足条件k＞7，
第五次运行k=5，S=11+5=16，不满足条件k＞7，
第六次运行k=6，S=16+6=22，不满足条件k＞7，
第七次运行k=7，S=22+7=29，不满足条件k＞7，
第八次运行k=8，S=29+8=37，此时满足条件k＞7，
输出S=37，
故选：D
点评：本题主要考查程序框图的识别和应用，了解程序的功能是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，有一个形如六边形的点阵，它的中心是一个点（算第1层），第2层每边有两个点，第3层每边有三个点，依此类推．如果一个六边形点阵共有169个点，那么它一共有已知函数f（x）=|1-
|（x＞0），当0＜a＜b，若f（a）=f（b）时，则有（ ）
| 1 |
| x |
| A、ab＞1 | ||
| B、ab≥1 | ||
C、ab≥
| ||
D、ab＞
|
若复数z=（a2+2a-3）+（a-l）i为纯虚数（i为虚数单位），则实数a的值为（ ）
| A、-3 | B、-3或1 |
| C、3或-1 | D、1 |
对于平面α，β，γ和直线a，b，m，n，下列命题中真命题是（ ）
| A、若a⊥m，a⊥n，m?α，n?α，则a⊥α |
| B、若α∥β，α∩γ=a，β∩γ=b则a∥b |
| C、若a∥b，b?α，则a∥α |
| D、若a?β，b?β，a∥α，b∥α，则β∥α |