题目内容
若双曲线C：2x2-y2=m（m＞0）与抛物线y2=8x的准线交于A，B两点，且|AB|=2
，则实数m的值为（ ）
| 3 |
| A、29 | B、20 | C、12 | D、5 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出抛物线的准线方程，根据双曲线方程，确定A，B两点的坐标，利用|AB|=2
，即可实数m的值．
| 3 |
解答：
解：∵抛物线y2=8x，2p=8，p=4，∴
=2．
∴抛物线的准线方程为x=-2．
设双曲线C：2x2-y2=m与抛物线的准线x=-2的两个交点A（-2，y），B（-2，-y）（y＞0），
则|AB|=|y-（-y）|=2y=2
，
∴y=
．
将x=-2，y=
代入双曲线C：2x2-y2=m，得2•（-2）2-3=m，
∴m=5．
故选：D．
| p |
| 2 |
∴抛物线的准线方程为x=-2．
设双曲线C：2x2-y2=m与抛物线的准线x=-2的两个交点A（-2，y），B（-2，-y）（y＞0），
则|AB|=|y-（-y）|=2y=2
| 3 |
∴y=
| 3 |
将x=-2，y=
| 3 |
∴m=5．
故选：D．
点评：本题考查抛物线，双曲线的几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
下列说法中正确的是（ ）
| A、“a=1”是直线“l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0平行”的充要条件 |
| B、命题“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x＞0” |
| C、命题“若m＞0，则方程x2+x-m=0有实数根”的逆否命题为：“若方程x2+x-m=0无实数根，则m≤0” |
| D、若p∧q为假命题，则p，q均为假命题 |
如果一个空间几何体的正视图、侧视图、俯视图都是半径等于5的圆，那么这个空间几何体的表面积等于（ ）
| A、100π | ||
B、
| ||
| C、25π | ||
D、
|
①若k＞0，则方程x2+2x-k=0有实根；
②“若a＞b，则ac＞bc”的否命题；
③“矩形的对角线相等”的逆命题；
④“若xy=0，则x、y至少有一个为零”的逆否命题．
以上命题中的真命题有（ ）
②“若a＞b，则ac＞bc”的否命题；
③“矩形的对角线相等”的逆命题；
④“若xy=0，则x、y至少有一个为零”的逆否命题．
以上命题中的真命题有（ ）
| A、①③ | B、①④ | C、②③ | D、③④ |
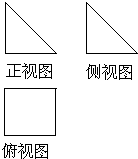一几何体的三视图如图所示，若正视图和侧视图都是等腰直角三角形，直角边长为1，则该几何体外接球的表面积为（ ）A、
| ||
| B、2π | ||
| C、3π | ||
| D、12π |
“a≥0，b≥0”是“
≥
”的（ ）
| a+b |
| 2 |
| ab |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充也不必要条件 |