题目内容
①若k＞0，则方程x2+2x-k=0有实根；
②“若a＞b，则ac＞bc”的否命题；
③“矩形的对角线相等”的逆命题；
④“若xy=0，则x、y至少有一个为零”的逆否命题．
以上命题中的真命题有（ ）
②“若a＞b，则ac＞bc”的否命题；
③“矩形的对角线相等”的逆命题；
④“若xy=0，则x、y至少有一个为零”的逆否命题．
以上命题中的真命题有（ ）
| A、①③ | B、①④ | C、②③ | D、③④ |
考点：命题的真假判断与应用
专题：简易逻辑
分析：由k的范围结合二次方程的判别式说明方程x2+2x-k=0有实根，判断①正确；
直接写出原命题的否命题、逆命题、逆否命题判断②③④的真假．
直接写出原命题的否命题、逆命题、逆否命题判断②③④的真假．
解答：
解：对于①，∵k＞0，则△=22+4k=4+4k＞0，
∴方程x2+2x-k=0有实根，命题①正确；
对于②，命题“若a＞b，则ac＞bc”的否命题为“若a≤b，则ac≤bc”为假命题；
对于③，“矩形的对角线相等”的逆命题为“对角线相等的四边形为矩形”，是假命题；
对于④，“若xy=0，则x、y至少有一个为零”的逆否命题为：“若x，y均不为零，则xy≠0”，是真命题．
∴以上命题中的真命题有①④．
故选：B．
∴方程x2+2x-k=0有实根，命题①正确；
对于②，命题“若a＞b，则ac＞bc”的否命题为“若a≤b，则ac≤bc”为假命题；
对于③，“矩形的对角线相等”的逆命题为“对角线相等的四边形为矩形”，是假命题；
对于④，“若xy=0，则x、y至少有一个为零”的逆否命题为：“若x，y均不为零，则xy≠0”，是真命题．
∴以上命题中的真命题有①④．
故选：B．
点评：本题考查命题的真假判断与应用，考查了一个命题的逆命题、否命题、逆否命题的写法与真假性判断，是中档题．
练习册系列答案
相关题目
若双曲线C：2x2-y2=m（m＞0）与抛物线y2=8x的准线交于A，B两点，且|AB|=2
，则实数m的值为（ ）
| 3 |
| A、29 | B、20 | C、12 | D、5 |
已知双曲线E：
-
=1（a，b＞0）的左焦点为F（-3，0），过点F的直线与E相交于A，B两点，若线段AB的中点为N（12，15），则E的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是（ ）
| A、梯形可以确定一个平面 |
| B、圆心和圆上两点可以确定一个平面 |
| C、两条直线a，b没有公共点，那么a与b是异面直线 |
| D、若a，b是两条直线，α，β是两个平面，且a?α，b?β，则a，b是异面直线 |
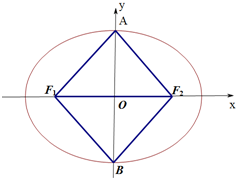如图，设椭圆C：